Transformation: Enlargement And Reduction

Enlargement (or reduction) is a transformation in which the size of an object is changed without changing its original shape. If the size of the object increase, we call it an enlargement and if the size of an object decrease, we call it a reduction.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

The enlargement is made with the help of a fixed point called centre of enlargement and by the fixed ratio called scale factor i.e. the ratio of the corresponding sides of the image and object. 

As enlargement changes the size of the object, it will have no real sense in case of a point.

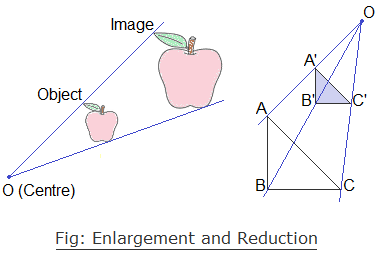
The following are the properties of enlargement:

1.   The object and the image under the enlargement are similar.

2.   Scale factor (k) =  

3.   If the scale factor k>1, then the transformation is called enlargement.

4.   If the scale factor 0<k<1, then the transformation is called reduction.

5.   If the scale factor k=1, then the transformation is identity.

6.   If the scale factor k<0, then the image will be on the opposite side of the object from the centre of enlargement.

Example 1: Find the image of ΔABC under the enlargement with the centre of enlargement O and scale factor 2. [It is denoted by E(O, 2)]

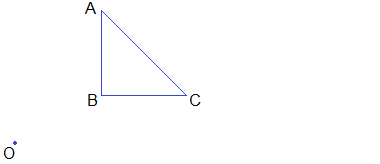
Solution:

For the image ΔABC under the given enlargement, perform the following steps:

Step 1: Join OA, OB and OC.

Step 2: Produce OA upto A’ such that OA’ = 2OA.

Step 3: Produce OB upto B’ such that OB’ = 2OB.

Step 4: Produce OC upto C’ such that OC’ = 2OC.

Step 5: Join A’B’, B’C’ and C’A’.

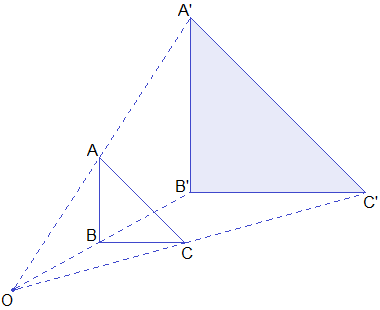
Hence, ΔA’B’C’ is the required image of ΔABC under the enlargement E(O, 2).

 

Example 2: Find the image of ΔPQR under the enlargement with centre of enlargement O and scale factor -½.

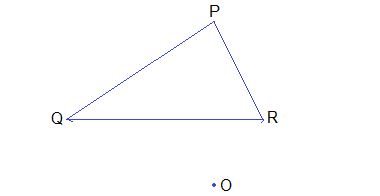
Solution:

As the scale factor is negative i.e. - ½, the image of ΔABC will be on the opposite side of centre O and the size will be half of the given figure. i.e. image of each side will be half of its corresponding object side.

Step 1: Join OP, OQ and OR.

Step 2: Produce PO upto P’ such that OP’ = ½OP.

Step 3: Produce QP and RO upto Q’ and R’ in the same direction so that OQ’ = ½ OQ and OR’ = ½OR.

Step 4: Join P’Q’, Q’R’ and R’P’.

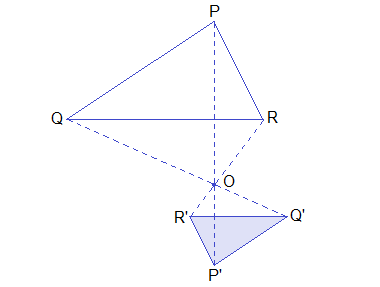
Hence, ΔP’Q’R’ is the image of ΔPQR under the given enlargement.

 

Enlargement Using Co-ordinates

The image under the enlargement with a given centre of enlargement and scale factor can be obtained with the help of co-ordinates.

Enlargement With Centre At Origin And Scale Factor k.

Let P(3, 1) and Q(2, 4) be two points and k = 2 be the scale factor and O(0, 0) be the centre of enlargement. Join OP and OQ and produce OP upto P’ such that OP’ = 2OP and produce OQ upto Q’ such that OQ’ = 2OQ and join P’Q’ which is the image of PQ. 

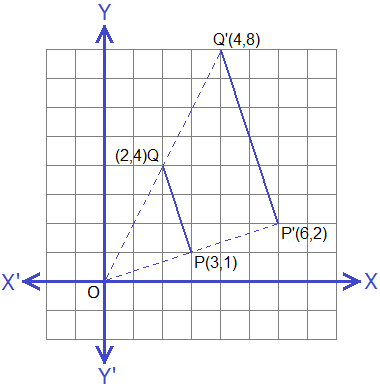
The co-ordinates of P’ and Q’ are (6, 2) and (4, 8) respectively.

       

Let us see the following table of some points in the plane and their corresponding images under the enlargement with centre O(0, 0) and scale factor k.

 

From the following table, we can see that the image of any point P(x, y) under the enlargement with centre O(0, 0) and scale factor k is P’(kx, ky),

       

 

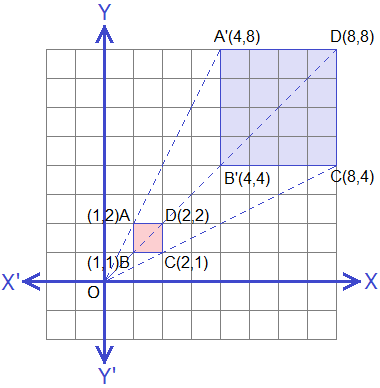
Example 3: If a square ABCD with vertices A(1, 2), B(1, 1), C(2, 1) and D(2, 2) is enlarged with the centre of enlargement O(0, 0) and scale factor 4. Find the co-ordinates of the vertices of the image square ABCD and draw ABCD and its image on the same graph paper.

Solution:

As the square ABCD has vertices A(1, 2), B(1, 1), C(2, 1) and D(2, 2), the image of these vertices under the enlargement with centre O(0, 0) and scale factor 4 can be obtained by using the formula,

Hence, the co-ordinates of image square A’B’C’D’ are A’(4, 8), B’(4, 4), C’(8, 4) and D’(8, 8). Drawing square ABCD and square A’B’C’D’ on the same graph paper we get the figure as shown:

 

Enlargement With Centre At Any Point M(a, b) And Scale Factor k.

The image of point P(x, y) under the enlargement with centre at any point M(a, b) and scale factor k can be derived by the following procedure.

Step 1: Draw a new co-ordinate axes X₁MX₁’ and Y₁MY₁’ having origin at M(a, b) and parallel to original axes.

Step 2: Find the co-ordinates of P(x, y) according to new co-ordinates axes i.e. P₁’(x-a, y-b).

Step 3: Find the image of P(x-a, y-b) under the enlargement with centre M(a, b) (origin of new axes) and scale factor k, which is P₁’[k(x-a), k(y-b)],

Step 4: Change the co-ordinates of image P’ to the original co-ordinate axes.

i.e.   P’[k(x-a), k(y-b)]

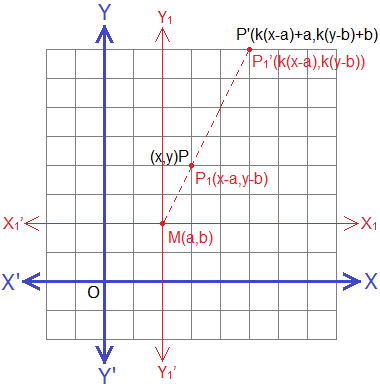
Hence, the image of P(x, y) under the enlargement with centre M(a, b) and scale factor k is given by P’[k(x-a)+a, k(y-b)+b], i.e.

Example 4: If ΔPQR with vertices P(-1, 2), Q(-1, -1) and R(1, 0) is enlarged with centre of enlargement M(1, 1) and scale factor -2. Find the co-ordinates of vertices of the image ΔPQR and draw ΔPQR and its image on the same graph paper.

Solution:

As P(-1, 2), Q(-1, -1) and R(1, 0) are the vertices of ΔPQR, the image of these vertices under the enlargement with centre M(1, 1) and scale factor -2 by using formula,

        

The vertices of image ΔP’Q’R’ under the given enlargement are P’(5, -1), Q’(5, 5) and R’(1, 3). Drawing ΔPQR and ΔP’Q’R’ on the same graph paper, we have the below figure.

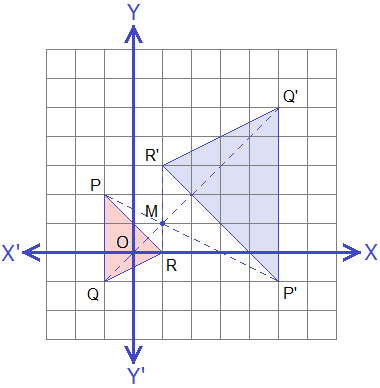
Example 5: If A(-1, -1), B(0, -3) and C(2, 0) are the vertices of ΔABC and ΔA’B’C’ is the image of ΔABC under the enlargement where A’(0, 2), B’(2, -2) and C’(6, 4). Find the centre and scale factor of this enlargement.

Solution:

As we have the co-ordinates of ΔABC and its image ΔA’B’C’ under the enlargement, we can find the centre and the scale factor of enlargement by drawing.

Step 1: Draw ΔABC and ΔA’B’C’ with the help of the given co-ordinates.

Step 2: Join AA’ and BB’ (or CC’) and produce them to meet each other at M.

Step 3: Co-ordinates of centre M is (-2, -4) and scale factor 

Hence, the required centre of enlargement is (-2, -4) and scale factor k = 2.

 

Alternative Method:

Let (a, b) be the centre and k be the scale factor of enlargement E. Under the enlargement,

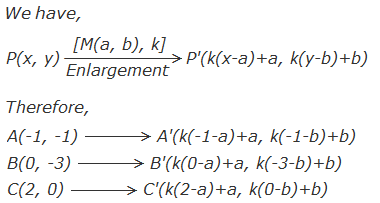
But, the vertices of image A’B’C’ are A’(0, 2), B’(2, 2) and C’(6, 4)

So,    k(-1-a)+a = 0 …………… (i)

        k(0-a)+a = 2 ……………. (ii)

        k(2-a)+a = 6 ……………. (iii)

and,  k(-1-b)+b = 2 ………….. (iv)

        k(-3-b)+b = 2 ………….. (v)

        k(0-b)+b = 4 …………… (vi)

Subtracting (i) from (ii), we get

        K = 2

Putting the value of k = 2 in (i)

        2(-1-a)+a = 0

or,    -2-2a+a = 0

or,    a = -2

Putting the value of k in (iv)

        2(-1-b)+b = 2

or,    -2-2b+b = 2

or,    b = -4

Hence, the centre of enlargement is (-2, -4) and scale factor 2.

If you have any questions or problems you can ask in the comments section below.

 

Was this article helpful? LIKE and SHARE it with friends…

Related Articles:

 

-       Transformation: Reflection

-       Transformation: Rotation

-       Transformation: Translation