Transformation: An Introduction

Transformation in sense of mathematics is the change of position, shape, or size of a geometric figure. A figure before the transformation is called an object and after transformation is called the image of the original object.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

In transformation, every point A of an object maps with a unique and distinct point A’ of the image, so it is a one-to-one function. 

If T is a transformation and A’ is the image point of A under T, then we denote it by T(A) = A’ or by T: A → A’ or simply by A → A’. 

If another transformation brings the image A’ back to the object (pre-image) point A, then such a transformation is called the inverse of the transformation T and it is denoted by T^-1.

Transformation sometimes leaves certain points unchanged. These points are said to be invariant under the given transformation. Any other features which are left unaltered by the transformation such as distance, angle, parallelism, etc. are also described as invariant.

Types of Transformation

If a transformation maps a point A to A itself, then it is called an Identity Transformation and it is denoted by I. So, I(A) = A. Identity transformation leaves all points unchanged.

If a transformation does not change the figure after transformation, then it called an Isometric Transformation. Isometric transformation maps a figure to a congruent image. It means object figure and image figure are congruent under the isometric transformation.

If a transformation changes the figure after transformation, then it is called a Non-Isometric Transformation. Non-isometric transformation maps a figure to a similar image. It means object figure and image figure are similar under non-isometric transformation.

There are four fundamental transformations:

A.   Reflection

B.   Rotation

C.   Translation

D.  Enlargement (or Reduction)

Reflection, Rotation, and Translation are isometric transformations and Enlargement (or Reduction) is a non-isometric transformation.

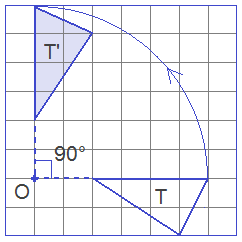
Study the following figures for the general concepts of Reflection, Rotation,  Translation, Enlargement, and Reduction. 

Reflection

Rotation

Enlargement

Reduction

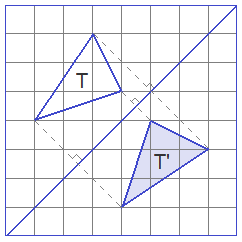
Visit the following pages for specific study on particular topics of transformation and related worked out examples:

- Reflection

- Rotation

- Translation

- Enlargement(or Reduction)

Do You Have Any Question?

If you have any queries regarding the topics, You can ask here in the comment section below.