Rotation is a transformation in which each point on
the object is rotated through an angle about a fixed point. The fixed point is
called the centre of rotation and
the angle is called the angle of
rotation.
Advertisement - Click Here!
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
There are two types of rotations on the
basis of directions:
1. Anticlockwise or Positive (+) rotation
2. Clockwise or Negative (–) rotation
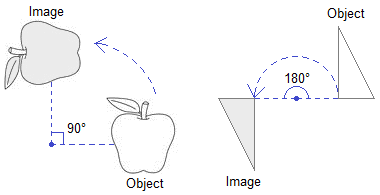
The following are the properties of rotation:
a. The object and the image under the rotation are congruent.
b. Every point on the object is rotated through same angle in the
same direction about centre of rotation to reach its image.
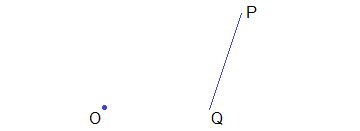
Example 1: Find the image of line PQ under the rotation through +90° about O.
Solution:
To find the image of line PQ under the rotation through +90°
about O, join OP and draw OP'⊥OP such that OP' = OP.
Similarly, join OQ and draw OQ'⊥OQ such that OQ' = OQ. And, join P'Q' as shown in the figure below.
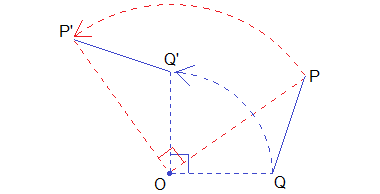
Hence P’Q’ is the image of PQ.
Example 2: Find the image of ΔPQR under the rotation through -70° (clockwise)
about O.
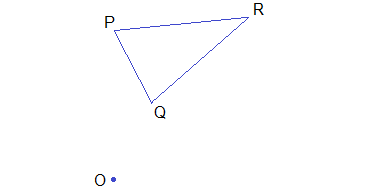
Solution:
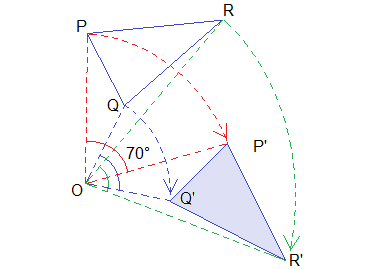
For the image of ΔPQR under the given rotation, join OP, OQ and OR by dotted lines as shown in the figure given below. Draw ∠POP' = ∠QOQ' = ∠ROR' = 70° toward clockwise (negative) direction such that OP' = OP, OQ' = OQ and OR' = OR. Then, join P'Q'R' which is the image of ΔPQR.
Example 3: If ΔP’Q’R’ be the image of the ΔPQR under the rotation, find the
centre and the angle of rotation.
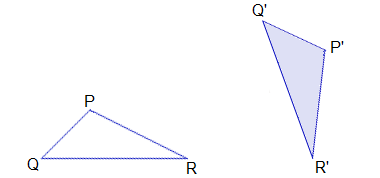
Solution:
Trace ΔPQR and ΔP’Q’R’ in the exercise book. Join PP’ and RR’ (or QQ’). Draw the perpendicular bisector of PP’ and RR’. Then the point of intersection of these two perpendicular bisectors i.e. O is the centre of rotation.
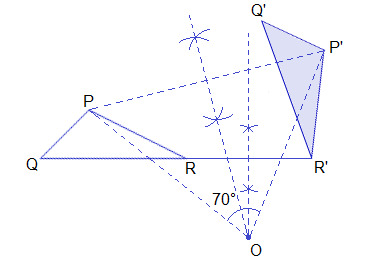
Now, join OP and OP’. The measure of ∠POP’ (70°) is the angle of rotation. The angle of rotation can also be the measure of ∠QOQ’ or ∠ROR’.
Rotation Using Co-ordinates
The image of the geometrical figures
under the rotation through 90°, 180° and 270° about a given point as the centre of
rotation can also be obtained with the help of co-ordinates.
Rotation through 90° About Origin (Positive Quarter Turn)
Let A(2, 3) be a point and O(0, 0) be the
centre of rotation and 90° be the angle of rotation. Join OA and draw OA'⊥OA (i.e ∠AOA’ = 90°) such that OA =
OA', then the co-ordinates of A’ will be (-3, 2) as shown in the graph given below.

Hence, A'(-3, 2) is the image of A(2, 3) under the rotation through +90° about origin O as shown in the figure.

Let us see the following table of some other points on the same graph and their corresponding images under the rotation through 90° about the origin.

From the above table, we can see that the image of point P(x, y) under the rotation through 90° about origin O is P’(-y, x)

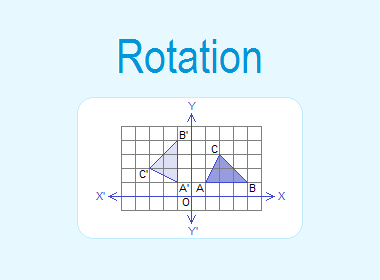
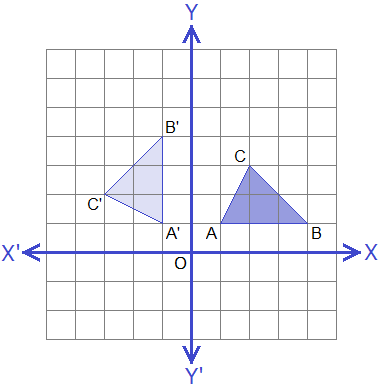
Example 4: If A(1, 1), B(4, 1) and C(2, 3) are the vertices of a triangle ABC,
find the co-ordinates of the vertices of the image of ΔABC under the rotation
through 90° about the origin and draw in a graph.
Solution:
As A(1, 1), B(4, 1) and C(2, 3) are the vertices of ΔABC, the
vertices of the image ΔA’B’C’ of ΔABC under the rotation through 90° about
origin can be obtained as follows:

Drawing ΔABC and its image ΔA’B’C’ on the graph paper, we have the figure as shown.
Rotation Through 180° About Origin (Half Turn)
Let A(2, 4) be a point and O(0, 0) be the centre of rotation and 180° be the angle of rotation. Join OA and produce AO to draw OA' (i.e ∠AOA’ = 180°) such that OA = OA', then the co-ordinates of A’ will be (-2, -4) as shown in the graph given below.

Hence, A'(-2, -4) is the image of A(2, 4) under the rotation through ±180° about the origin.

Let us see the following table of some other points on the same graph and their corresponding images under the rotation through 180° about origin.
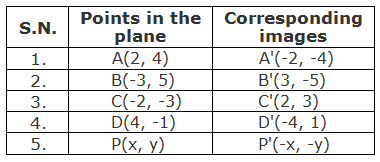
From the above table, we can see that the image of point P(x, y) under the rotation through 180° about origin is P’(-x, -y)

Rotation Through 270° (or -90°) About Origin (Negative Quarter Turn)
Let A(-4, -3) be a point and O(0, 0) be the centre of rotation and 270° (-90°) be the angle of rotation. Join OA and draw OA'⊥OA (i.e reflex ∠AOA’ = 270°) such that OA = OA', then the co-ordinates of A’ will be (-3, 4) as shown in the graph given below.

Hence, A'(-3, 4) is the image of A(-4, -3) under the rotation through 270° (-90°) about origin O.

Let us see the following table of some other points on the sane graph and their corresponding images under the rotation through 270° about origin.
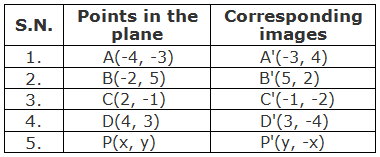
From the above table, we can see that the image of a point P(x, y) under the rotation through 270° about origin O(0, 0) is P’(y, -x)

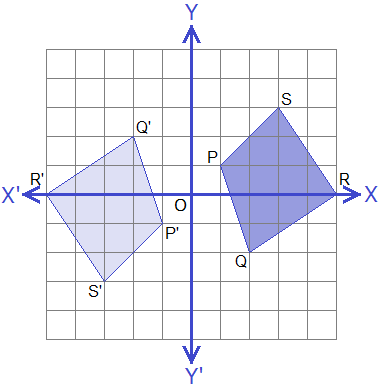
Example 5: If P(1, 1), Q(2, -2), R(5, 0) and S(3, 3) are the vertices of a
given quadrilateral PQRS, find the co-ordinates of the vertices of its image
under the rotation through 180° about origin. Also, draw object and image on the
same graph paper.
Solution:
As P(1, 1), Q(2, -2), R(5, 0) and S(3, 3) are the vertices of
given quadrilateral PQRS, the co-ordinates of the vertices of its image under
the rotation through 180° about origin can be obtained as follows:
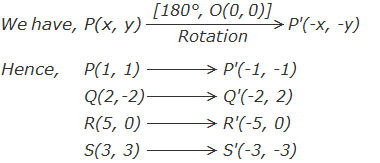
We can draw the quadrilateral PQRS and its image P’Q’R’S’ on the same graph as given below.
Rotation Through 90° About Any Point (a, b)
Let A(4, 5) be a point and M(2, 1) be the centre of rotation and 90° be the angle of rotation. Join MA and draw MA'⊥MA (i.e ∠AMA’ = 90°) such that MA = MA', then the co-ordinates of A’ will be (-2, 3) as shown in the graph given below.
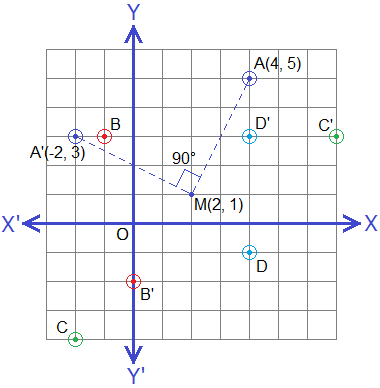
Hence, A'(-2, 3) is the image of A(4, 5) under the rotation through +90° about a point M(2, 1).

Let us see the following table of some other points on the same graph and their corresponding images under the roration through 90° about M(2, 1) as the centre of rotation.
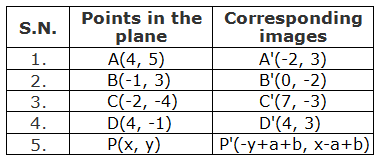
From the above table, we can see that the image of a point P(x, y) under the rotation through +90° about M(a, b) is given by P’(-y+a+b, x-a+b).

Rotation Through 180° About Any Point M(a, b)
Let A(5, 4) be a point and M(2, 1) be the centre of rotation and 180° be the angle of rotation. Join MA and produce AM to draw MA' (i.e ∠AMA’ = 180°) such that MA = MA', then the co-ordinates of A’ will be (-1, -2) as shown in the graph given below.
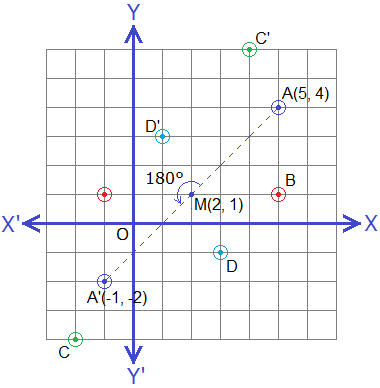
Hence, A'(-1, -2) is the image of A(5, 4) under the rotation through ±180° about a point M(2, 1).

Let us see the following table of some other points on the same graph and their corresponding images under the rotation through 180° about M(2, 1) as the centre of rotation.

From the above table, we can see that the image of a point P(x, y) under the rotation through 180° about M(a, b) is P’(-x+2a, -y+2b).

Rotation Through 270° About Any Point M(a, b)
Let A(5, 2) be a point and M(2, 1) be the centre of rotation and 270° (-90°) be the angle of rotation. Join MA and draw MA'⊥MA (i.e reflex ∠AMA’ = 270°) such that MA = MA', then the co-ordinates of A’ will be (3, -2) as shown in the graph given below.
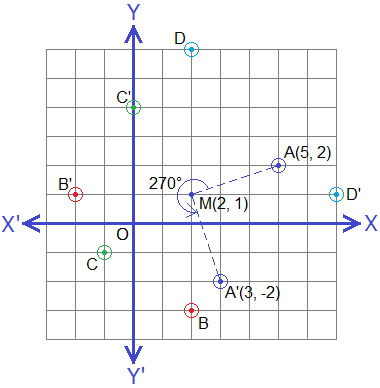
Hence, A'(3, -2) is the image of A(5, 2) under the rotation through 270° (-90°) about a point M(2, 1).
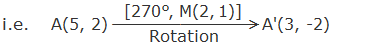
Let us see the following table of some other points on the same graph and their corresponding images under the rotation through 270° about M(2, 1) as the centre of rotation.

From the above table, we can see that the image of a point P(x, y) under the rotation through 270° about M(a, b) is P’(y-b+a, -x+a+b).

Conclusion About Rotation Using Co-ordinates
In conclusion, we have the following formulae for the rotation using co-ordinates:

Example 6: If the vertices of a quadrilateral ABCD are A(1, 2), B(3, 3), C(2,
5) and D(-1, 5). Find the co-ordinates of the vertices of the image of ABCD
under the rotation through -90° about M(-2, 2) and draw in a graph.
Solution:
As A(1, 2), B(3, 3), C(2, 5) and D(-1, 5) are the vertices of a quadrilateral ABCD, the co-ordinates of the vertices of its image under the rotation through -90° i.e. 270° about M(-2, 2) can be obtained by using the formula as follows:
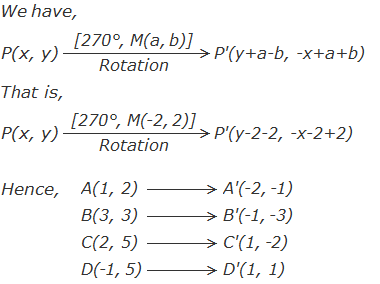
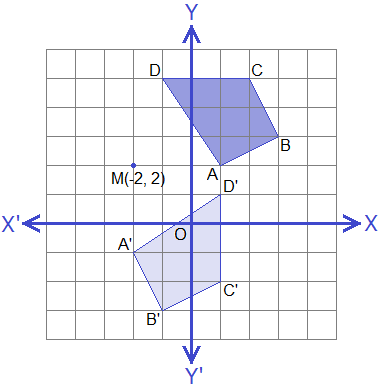
We can draw the quadrilateral ABCD and its image A’B’C’D’ on the same graph as shown below.
Do you have any questions regarding the Rotation?
You can ask your questions or problems here in the comment section below.



0 comments: