
Scalene Triangle
A triangle having non of the sides equal is called an
scalene triangle. In the given figure of triangle ABC, all three sides AB, BC
and AC have different measurements, therefore ΔABC is a scalene triangle.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Area of Scalene Triangle (Heron’s
Formula)
If all sides of a scalene triangle are given, then we can
find out the area of the triangle by Heron’s formula. Heron of Alexandria gave
this formula.
Let a, b and c be three sides BC, AC and AB respectively of a
scalene triangle ABC given in the figure. AD is the height which is denoted by
h.
Let, BD=x, then DC= a – x
Perimeter of ΔABC = a + b + c
Let, 2s = a + b + c where s = semi-perimeter
Area of ΔABC = ½ a × h ………...... (i) [Because, Area of Δ = ½ × base × height]
In right angled ΔADC,
In the right angled ΔADB,
From (i) and (ii),
Substituting the value of x from above in equation
(iii), we get
Putting the value of h in equation (i),
we get
Thus, when three sides of a triangle are
given, then its area is given by the formula
where a, b and c are the three sides of
the triangle and s is the semi perimeter i.e.
This formula is known as the Heron’s
formula.
Workout Examples
Example 1: Find the area of triangle ABC.
Solution:
In ΔABC, a = 10cm
b = 8cm
c = 6cm
You can comment your questions or problems regarding the scalene triangle or area of triangles here.









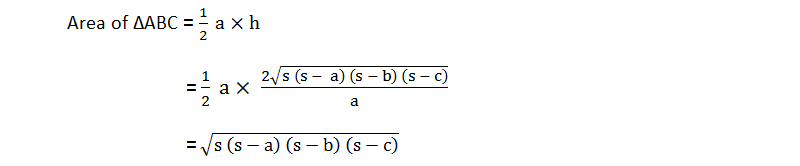




0 comments: