Area of triangle
Total surface
covered by a triangle is called the area of triangle. To find the area of a
triangle we can do the following activities:
i. Take a
paper in triangle shape of base (b) and height (h) as shown in the figure.
ii. Cut
horizontally through middle of the perpendicular as shown in figure.
iii. Cut
upper part into two small triangles through perpendicular as shown in the
figure.
iv. Arrange the
small triangles in one place to form a rectangle ABCD as shown in the figure.
v. The
rectangle ABCD so formed will have the length equal to b and breadth equal to
h/2 as shown in the figure.
∴ Area of Δ = Area of rectangle ABCD
= BC × CD
= b × h/2
= ½ × b × h
∴ Area of Δ = ½ × b × h
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Area
of a right angled triangle
When
the triangle is a right angled triangle then height (h) = perpendicular (p),
therefore the area of triangle = ½ × base × perpendicular
i.e area of Δ = ½ × b × p
Area
of an equilateral triangle
In
the given figure, ΔABC is an equilateral triangle and AM⊥BC.
If AB
= BC = AC = a then BM = CM = a/2
Area
of an isosceles triangle
In
isosceles ΔABC, AB = AC = a and base BC = b
Then
AM⊥BC is drawn. Thus BM = CM = b/2
Area of scalene triangle
If a,
b and c are three sides of a scalene triangle then
Workout Examples
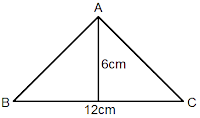
Example 1: Find area of the triangle given below:
Solution:
From the figure,
Base (b) = 12 cm
Height(h) = 6 cm
we know,
Area
of triangle = ½ × b × h
= ½ × 12cm × 6 cm
= 36 cm2
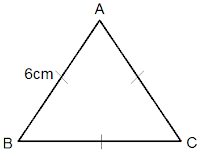
Example 2:
Solution:
Given figure is an
equilateral triangle where
a = 6 cm
we know,
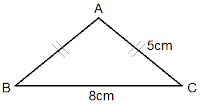
Example 3: Find the area of the triangle given below:
Solution:
Given figure is an
isosceles triangle where
Base(b) = 8 cm
Two equal sides (a)
= 5 cm
we know,
Example 4: Find the area of the triangle
ABC given below.
Solution:
In triangle ABC,
a=10cm, b=8cm and c=6cm
0 comments: