Vectors and it's Components

0 comments
Vectors and its Components

Vectors: Introduction


The quantities which can be measured are called physical quantities. Some physical quantities have magnitudes only but some physical quantities have magnitudes as well as directions.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************


Let us study the addition of some physical quantities. For example, if we have two rectangles of areas 6cm2 and 8cm2, the total areas of these two rectangles is (6 + 8)cm2 i.e. 14cm2.

Sum of areas of two rectangles of area 6cm2 and 8cm2 is equal to 14cm2.

If two forces 4N and 5N act on a body, what is the total force acting on the body, 9N or 1N? Its answer is uncertain unless their directions are known. If two forces have same direction the total force on the body is 4N + 5N = 9N.

Sum (or resultant force) of two forces 4N and 5N acting toward the same direction is 9N i.e. 4N + 5N = 9N.

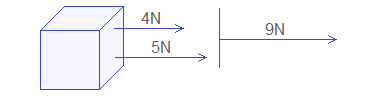
If two forces have opposite direction the total force on the body is 5N – 4N = 1N.

Sum (or resultant force) of two forces 4N and 5N acting toward the opposite direction is 1N i.e. 5N + (-4N) = 1N.

In the calculation of some physical quantities, the direction has very important role.



Scalars and Vectors


Scalar Quantity: A physical quantity which can be measured with its magnitude only is known as a scalar quantity. For example: mass, length, area, volume etc.


Vector Quantity: A physical quantity which can be measured with its magnitude as well as direction is known as a vector quantity. For example: velocity, acceleration, force etc.

Vector Notation


A vector is denoted by a letter or a combination of two letters with an arrow over it. For example: a ⃗, (AB) ⃗ etc. are vectors. But a letter or a combination of two letters without an arrow over it is a scalar. For example: a, AB etc.


Representation of a vector


A vector is generally represented by a directed line segment. The length of the line segment is chosen according to some scale to represent the magnitude and the arrow to represent the direction of the vector.

A vector from point A to point B is denoted by (AB) ⃗. (Figure of vector (AB) ⃗) We call the point A, the initial (starting) point or tail and B, the terminal (end) point or head of the vector (AB) ⃗. A vector is also represented by components form. (Figure of vector (AB) ⃗ in components form) A vector from point P to Q is denoted by (■(x@y)) = (■(PM@MQ)), where PM = x is called x-component and QM = y is called y-component.


Directed Line Segments


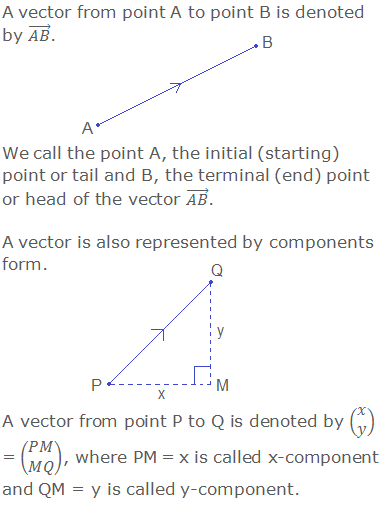
“If two points of a line are taken, one as the initial point and another as the terminal point, then it is called a directed line segment.”

(Figure of vector (MN) ⃗) If (MN) ⃗ is a directed line segment, then |(MN) ⃗| represents the length and arrow (→) shows the direction (i.e. from M to N). The two ends of directed line segments are not interchangeable. So the directed line segments (AB) ⃗ and (BA) ⃗ are not the same. (Figure of vectors (AB) ⃗ and (BA) ⃗) These directed line segments are equal in magnitude but opposite in direction. So, (AB) ⃗ = - (BA) ⃗.

If the length and direction of two directed line segments are same, they are called equivalent directed line segments or equal directed line segments. In the figure given below

(Figure of vectors (CD) ⃗ and (PQ) ⃗) a) (CD) ⃗ and (PQ) ⃗ have the same direction. b) (CD) ⃗ and (PQ) ⃗ have the same length. Hence, (CD) ⃗ = (PQ) ⃗. (Figure of vector (PQ) ⃗ + (QR) ⃗ = (PR) ⃗) In the figure above, the terminal point of (PQ) ⃗ and initial point of (QR) ⃗ are the same. The initial point of (PQ) ⃗ + (QR) ⃗ is P and its terminal point is R. Hence, (PQ) ⃗ + (QR) ⃗ = (PR) ⃗ (Figure of vector (AC) ⃗ = 2(AB) ⃗) As in the figure above, if (AB) ⃗ and (BC) ⃗ are two equal directed line segments i.e. (AB) ⃗ = (BC) ⃗, then, (AC) ⃗ = (AB) ⃗ + (BC) ⃗ or, (AC) ⃗ = (AB) ⃗ + (AB) ⃗ or, (AC) ⃗ = 2(AB) ⃗ Here, directed line segment (AC) ⃗ is expressed in terms of (AB) ⃗. In general, if k is any number and (AB) ⃗ be a directed line segment, then k(AB) ⃗ represent another directed line segment (AC) ⃗ such that, a) C lies in the direction of (AB) ⃗ if k > 0 and, |(AC) ⃗| = k|(AB) ⃗|. b) C lies in the opposite direction of (AB) ⃗ if k < 0 and, |(AC) ⃗| = –k|(AB) ⃗|.


Position Vector

A point P(x, y) determines its position with reference to origin O(0, 0). Join OP, draw PN⊥OX, so ON = x and PN = y.

To displace from O to N and again from N to P is same as to displace from O to P. This horizontal displacement (ON) ⃗ with ON = x and vertical displacement (NP) ⃗ with NP = y combinely gives the displacement (OP) ⃗. The displacement (OP) ⃗ is written as (x, y) or (■(x@y)). Here, (OP) ⃗ is said to be the position vector of P. Here x and y are said to be x-component (horizontal component) and y-component (vertical component) of (OP) ⃗ respectively. ∴ The position vector of point P(x, y) is (OP) ⃗ = (■(x@y)).


Vectors in Terms of Components


Let P(x1, y1) and Q(x2, y2) be two points on the plane. From P and Q draw PM⊥OX and QN⊥OX and again draw PR⊥QN.

Let P(x1, y1) and Q(x2, y2) be two points on the plane. From P and Q draw PM⊥OX and QN⊥OX and again draw PR⊥QN. Here, PR = MN = ON – OM = x2 – x1 and QR = QN – RN = QN – PM = y2 – y1. The displacement vector (PQ) ⃗ has horizontal displacement (PR) ⃗ and vertical displacement (RQ) ⃗. Hence, (PQ) ⃗ = (x2 – x1, y2 – y1) or (■(x_2-x_1@y_2-y_1 )). Here, we have position vectors of P and Q are (OP) ⃗ = (■(x_1@y_1 )) and (OQ) ⃗ = (■(x_2@y_2 )). So, (PQ) ⃗ = (■(x_2-x_1@y_2-y_1 )) = (■(x_2@y_2 )) + (■(x_1@y_1 )) = (OQ) ⃗ – (OP) ⃗. ∴ (PQ) ⃗ = (OQ) ⃗ – (OP) ⃗ i.e. The vector joining two points P(x1, y1) and Q(x2, y2) is (PQ) ⃗ = (OQ) ⃗ – (OP) ⃗ = (■(x_2-x_1@y_2-y_1 )).


Worked Out Examples

Example 1: Find the vectors represented by the following line segments in component form.

Vectors (AB) ⃗, (CD) ⃗, (PQ) ⃗ and (MN) ⃗ in a graph.

Solution: In the above graph,

For vector (AB) ⃗: Starting from A, horizontal component (right) = 3 and, vertical component (up) = 1. Hence, (AB) ⃗ = (■(3@1)). For vector (CD) ⃗: Starting from C, horizontal component (left) = -3 and, vertical component (up) = 2. Hence, (CD) ⃗ = (■(-3@2)). For vector (PQ) ⃗: Starting from P, horizontal component (left) = -2 and, vertical component (below) = -2. Hence, (PQ) ⃗ = (■(-2@-2)). For vector (MN) ⃗: Starting from M, horizontal component (right) = 2 and, vertical component (below) = -3. Hence, (MN) ⃗ = (■(2@-3)).


Example 2: Represent the following vectors by the directed line segments.

a) (AB) ⃗ = (■(2@-2)) b) (CD) ⃗ = (■(-2@-3)) c) (PQ) ⃗ = (■(-4@2)) d) (MN) ⃗ = (■(4@2)) Solution: (AB) ⃗ = (■(2@-2)) Here, Horizontal component = +2 and, Vertical component = -2. ∴ Starting from A, 2 units right and then 2 units down will the point B be. (Figure of vector (AB) ⃗ = (■(2@-2)) in a graph) Similarly the directed line segments: b. (CD) ⃗ = (■(-2@-3)), c. (PQ) ⃗ = (■(-4@2)) and d. (MN) ⃗ = (■(4@2)) can be drawn as shown in the figure. (Figure of vectors (CD) ⃗ = (■(-2@-3)), (PQ) ⃗ = (■(-4@2)) and (MN) ⃗ = (■(4@2)) in a graph)

Do you have any questions regarding the vectors and it's components?


You can ask your questions or problems here, in the comment section below.

Labels:

0 comments:

Subscribe to: Post Comments (Atom)