Vector Operations

0 comments
Vector Operations

Vector Operations: The vectors can be added, subtracted or multiplied with one another. Addition of vectors, difference of vectors, multiplication of a vector by a scalar, product of vectors, etc. are called vector operations.




********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************


Addition of Vectors


Consider two vectors ( "a" ) ⃗ and ( "b" ) ⃗ and place them making head of ( "a" ) ⃗ together with tail of ( "b" ) ⃗, then the third vector from the tail of ( "a" ) ⃗ to the head of ( "b" ) ⃗ will be obtained. The third vector is the sum of ( "a" ) ⃗ and ( "b" ) ⃗ and is denoted by ( "a" ) ⃗ + ( "b" ) ⃗. The sum is called the resultant of two vectors.


Study the following three cases:


Case I:

When ( "a" ) ⃗ and ( "b" ) ⃗ are like vectors, then the sum of ( "a" ) ⃗ and ( "b" ) ⃗ is vector in their direction with the magnitude as the sum of their magnitudes.

Case II:

When ( "a" ) ⃗ and ( "b" ) ⃗ are unlike vectors, then the sum of ( "a" ) ⃗ and ( "b" ) ⃗ is vector in the direction of the greater vector with the magnitude as the difference of their magnitudes.

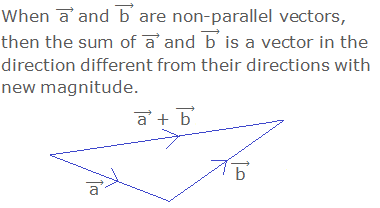
Case III:

When ( "a" ) ⃗ and ( "b" ) ⃗ are non-parallel vectors, then the sum of ( "a" ) ⃗ and ( "b" ) ⃗ is a vector in the direction different from their directions with new magnitude.

Triangle Law of Vector Addition


In the given figure, ("AB" ) ⃗ displaces a point from A to B and ("BC" ) ⃗ displaces the same point from B to C, then the total displacement of ("AB" ) ⃗ and ("BC" ) ⃗ is the displacement from A to C, which is denoted by ("AC" ) ⃗. Hence, ("AB" ) ⃗ + ("BC" ) ⃗ = ("AC" ) ⃗. This is called Triangle Law of Vector Addition.

Definition:


The triangle law of vector addition states that: “If the magnitude and direction of two vectors are represented by two sides of a triangle taken in order, then the magnitude and direction of their sum is given by the third side taken in reverse order.”

Parallelogram Law of Vector Addition


Let ("AB" ) ⃗ = ( "a" ) ⃗ and ("AC" ) ⃗ = ( "b" ) ⃗ be two co-initial vectors completing parallelogram ABCD by taking AB and AC as adjacent sides and join diagonal AD of parallelogram ABCD. By the property of parallelogram, ("CD" ) ⃗ = ("AB" ) ⃗ = ( "a" ) ⃗ and ("BD" ) ⃗ = ("AC" ) ⃗ = ( "b" ) ⃗. Now from ΔABD, ("AD" ) ⃗ = ("AB" ) ⃗ + ("BD" ) ⃗ [By Triangle law of vector addition] i.e. ("AD" ) ⃗ = ( "a" ) ⃗ + ( "b" ) ⃗ This is called Parallelogram Law of Vector Addition.

Definition:


The parallelogram law of vector addition states that: “If two adjacent sides of a parallelogram through a point represents two vectors in magnitude and direction, then their sum is given by the diagonal of the parallelogram through the same point in magnitude and direction.”


 

Polygon Law of Vector Addition


In polygon ABCDE, the sum of vectors represented by ("AB" ) ⃗, ("BC" ) ⃗, ("CD" ) ⃗ and ("DE" ) ⃗ taken in order is equal to the vector represented by ("AE" ) ⃗. Proof: Join AC and AD. Now, using vector addition, ("AC" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ And, ("AD" ) ⃗ = ("AC" ) ⃗ + ("CD" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ + ("CD" ) ⃗ Now, ("AE" ) ⃗ = ("AD" ) ⃗ + ("DE" ) ⃗ Or, ("AE" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ + ("CD" ) ⃗ + ("DE" ) ⃗ ∴ ("AE" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ + ("CD" ) ⃗ + ("DE" ) ⃗ This is called Polygon Law of Vector Addition.

Definition:


The polygon law of vector addition states that: “If a number of vectors can be represented in magnitude and direction by the sides of polygon taken in order, their sum is given in magnitude and direction by the closing side of the polygon taken in reverse order.”

Addition of Two Vectors in Components Form


Suppose ( "a" ) ⃗ = (■(x_1@y_1 )) and ( "b" ) ⃗ = (■(x_2@y_2 )) be two vectors then the sum of vectors ( "a" ) ⃗ and ( "b" ) ⃗ is denoted by ( "a" ) ⃗ + ( "b" ) ⃗ and is defined as ( "a" ) ⃗ + ( "b" ) ⃗ = (■(x_1@y_1 )) + (■(x_2@y_2 )) = (■(x_1+x_2@y_1+y_2 )).


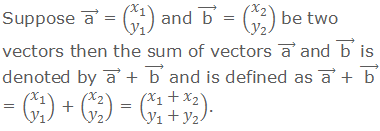
Geometrical Proof:


Let ( "a" ) ⃗ = (■(x_1@y_1 )) and ( "b" ) ⃗ = (■(x_2@y_2 )) be two vectors. Draw ( "OA" ) ⃗ = ( "a" ) ⃗ = (■(x_1@y_1 )) and ( "OB" ) ⃗ = ( "b" ) ⃗ = (■(x_2@y_2 )) as shown in the figure. Construct a parallelogram OACB with OA and OB as adjacent sides and join OC. Draw BM⊥OX, AN⊥OX, CL⊥OX and AK⊥CL. Now, ΔOBM ≅ ΔCAK (Proof is omitted) ∴ OM = AK = NL = x2 and BM = CK = y2 ∴ OL = x1 + x2 and CL = y1 + y2 ∴ C = (x_1+x_2, y_1+y_2) ∴ ( "OC" ) ⃗ = (■(x_1+x_2@y_1+y_2 )) From the addition of directed line segments, ("OC" ) ⃗ = ("OA" ) ⃗ + ("AC" ) ⃗ = ( "a" ) ⃗ + ( "b" ) ⃗ Hence, ( "a" ) ⃗ + ( "b" ) ⃗ = (■(x_1+x_2@y_1+y_2 )). Proved.


Subtraction of Vectors


Let (AB) ⃗ = ( "a" ) ⃗ and ("BC" ) ⃗ = ( "b" ) ⃗ be two vectors. The addition of ( "a" ) ⃗ and ( "b" ) ⃗ is denoted by ("AC" ) ⃗. The difference between ( "a" ) ⃗ and ( "b" ) ⃗ is the sum of ( "a" ) ⃗ and -( "b" ) ⃗. In the adjoining figure of ΔABC, draw BD such that BD = BC then ("BD" ) ⃗ = -("BC" ) ⃗ = -( "b" ) ⃗. Now, by triangle law of vector addition, ("AC" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ = ( "a" ) ⃗ + ( "b" ) ⃗. Again, ("AD" ) ⃗ = ("AB" ) ⃗ + ("BD" ) ⃗ = ( "a" ) ⃗ + (-( "b" ) ⃗) = ( "a" ) ⃗ – ( "b" ) ⃗, which is the subtraction of vectors. Note: If ( "a" ) ⃗ = (■(x_1@y_1 )) and ( "b" ) ⃗ = (■(x_2@y_2 )) then ( "a" ) ⃗ – ( "b" ) ⃗ = (■(x_1-x_2@y_1-y_2 )).


Multiplication of a Vector by a Scalar


Let ( "a" ) ⃗ = (■(x_1@y_1 )), then 2( "a" ) ⃗ = ( "a" ) ⃗ + ( "a" ) ⃗ = (■(x_1@y_1 )) + (■(x_1@y_1 )) = (■(x_1+x_1@y_1+y_1 )) = (■(〖2x〗_1@〖2y〗_1 )). Here, the vectors ( "a" ) ⃗ and 2( "a" ) ⃗ are parallel and the magnitude of 2( "a" ) ⃗ is double the magnitude of ( "a" ) ⃗. So, in general, if ( "a" ) ⃗ = (■(x_1@y_1 )) be a vector and k be a scalar, then k( "a" ) ⃗ = (■(〖kx〗_1@ky_1 )). And, the vector k( "a" ) ⃗ is parallel to vector ( "a" ) ⃗ and its magnitude is k times the magnitude of ( "a" ) ⃗. Note: If k > 0, the direction of k( "a" ) ⃗ lies in the direction of ( "a" ) ⃗. If k < 0, the direction of k( "a" ) ⃗ lies in the opposite direction of ( "a" ) ⃗. This is called multiplication of a vector by a scalar.


Unit Vectors i And j


Let O be the origin and OX and OY be the positive X-axis and Y-axis respectively. Then the unit vectors along X-axis and Y-axis are denoted by ( "i" ) ⃗ and ( "j" ) ⃗ respectively and are defined by ( "i" ) ⃗ = (■(1@0)) and ( "j" ) ⃗ = (■("0" @"1" )). Every vector (■(x@y)) can be represented by x( "i" ) ⃗ + y( "j" ) ⃗ and conversely. Here, ( "i" ) ⃗ = (■(1@0)) and ( "j" ) ⃗ = (■(0@1)) Then, x( "i" ) ⃗ + y( "j" ) ⃗ = x (■(1@0)) + y (■(0@1)) = (■(x@0)) + (■(0@y)) = (■(x@y)) Conversely, (■(x@y)) = (■(x@0)) + (■(0@y)) = x (■(1@0)) + y (■(0@1)) = x( "i" ) ⃗ + y( "j" ) ⃗

Worked Out Examples


Example 1: If ( "a" ) ⃗ = (■(2@-5)) and ( "b" ) ⃗ = (■(2@3)), find ( "a" ) ⃗ + ( "b" ) ⃗ and ( "a" ) ⃗ – ( "b" ) ⃗ and show in a squared paper. Solution: Here, ( "a" ) ⃗ = (■(2@-5)) and ( "b" ) ⃗ = (■(2@3)) ∴ ( "a" ) ⃗ + ( "b" ) ⃗ = (■(2@-5)) + (■(2@3)) = (■(2+2@-5+3)) = (■(4@-2)) ∴ ( "a" ) ⃗ – ( "b" ) ⃗ = (■(2@-5)) – (■(2@3)) = (■(2-2@-5-3)) = (■(0@-8))


Example 2: If ( "a" ) ⃗ = (■(2@5)) and ( "b" ) ⃗ = (■(6@15)), show that ( "a" ) ⃗ and ( "b" ) ⃗ are parallel. Solution: Here, ( "a" ) ⃗ = (■(2@5)) and ( "b" ) ⃗ = (■(6@15)) ( "b" ) ⃗ = (■(6@15)) = (■(3×2@3×5)) = 3 (■(2@5)) = 3( "a" ) ⃗ ∴ ( "b" ) ⃗ = 3( "a" ) ⃗ Which shows that ( "a" ) ⃗ and ( "b" ) ⃗ are parallel.


Example 3: If ( "a" ) ⃗ = (■(2@-3)) and ( "b" ) ⃗ = (■(-4@2)), find 2( "a" ) ⃗ – ( "b" ) ⃗. Also find the magnitude of 2( "a" ) ⃗ – ( "b" ) ⃗ and unit vector along 2( "a" ) ⃗ – ( "b" ) ⃗. Solution: Here, ( "a" ) ⃗ = (■(2@-3)) and ( "b" ) ⃗ = (■(-4@2)) ∴ 2( "a" ) ⃗ – ( "b" ) ⃗ = 2 (■(2@-3)) – (■(-4@2)) = (■(4@-6)) – (■(-4@2)) = (■(4+4@-6-2)) = (■(8@-8)) ∴ Magnitude of 2( "a" ) ⃗ – ( "b" ) ⃗ = |2( "a" ) ⃗ – ( "b" ) ⃗| = √(8^2+〖(-8)〗^2 ) = 8√2 units. ∴ Unit vector along 2( "a" ) ⃗ – ( "b" ) ⃗ = (2( a ) ⃗ – ( b ) ⃗)/(|2( "a" ) ⃗ – ( "b" ) ⃗|) = 1/(8√2) (■(8@-8)) = (■(1/√2@-1/√2))


Example 4: If ( "a" ) ⃗ = (■(-2@-4)) and 2( "a" ) ⃗ + 3( "b" ) ⃗ = (■(2@3)), find ( "b" ) ⃗. Solution: Here, ( "a" ) ⃗ = (■(-2@-4)) and let ( "b" ) ⃗ = (■(x@y)) We have, 2( "a" ) ⃗ + 3( "b" ) ⃗ = (■(2@3)) i.e. 2(■(-2@-4)) + 3(■(x@y)) = (■(2@3)) or, (■(-4@-8)) + 3(■(x@y)) = (■(2@3)) or, 3(■(x@y)) = (■(2@3)) – (■(-4@-8)) or, 3(■(x@y)) = (■(2+4@3+8)) or, 3(■(x@y)) = (■(6@11)) or, (■(x@y)) = 1/3 (■(6@11)) or, (■(x@y)) = (■(2@11/3)) ∴ ( "b" ) ⃗ = (■(2@11/3)).


Example 5: In the given figure, the diagonals PR and QS of a quadrilateral PQRS intersect at O. If ("OP" ) ⃗ = ( "a" ) ⃗, ("OQ" ) ⃗ = ( "b" ) ⃗, ("OR" ) ⃗ = ( "c" ) ⃗, ("OS" ) ⃗ = ( "d" ) ⃗, prove that ("PQ" ) ⃗ + ("QR" ) ⃗ + ("RS" ) ⃗ + ("SP" ) ⃗ = 0. Solution: Here, ("PO" ) ⃗ = -("OP" ) ⃗ = -( "a" ) ⃗, ("QO" ) ⃗ = -("OQ" ) ⃗ = -( "b" ) ⃗, ("RO" ) ⃗ = -("OR" ) ⃗ = -( "c" ) ⃗ and, ("SO" ) ⃗ = -("OS" ) ⃗ = -( "d" ) ⃗ Now, ("PQ" ) ⃗ = ("PO" ) ⃗ + ("OQ" ) ⃗ = -( "a" ) ⃗ + ( "b" ) ⃗ = ( "b" ) ⃗ – ( "a" ) ⃗ ("QR" ) ⃗ = ("QO" ) ⃗ + ("OR" ) ⃗ = -( "b" ) ⃗ + ( "c" ) ⃗ = ( "c" ) ⃗ – ( "b" ) ⃗ ("RS" ) ⃗ = ("RO" ) ⃗ + ("OS" ) ⃗ = -( "c" ) ⃗ + ( "d" ) ⃗ = ( "d" ) ⃗ – ( "c" ) ⃗ ("SP" ) ⃗ = ("SO" ) ⃗ + ("OP" ) ⃗ = -( "d" ) ⃗ + ( "a" ) ⃗ = ( "a" ) ⃗ – ( "d" ) ⃗ ∴ ("PQ" ) ⃗ + ("QR" ) ⃗ + ("RS" ) ⃗ + ("SP" ) ⃗ = ( "b" ) ⃗ – ( "a" ) ⃗ + ( "c" ) ⃗ – ( "b" ) ⃗ + ( "d" ) ⃗ – ( "c" ) ⃗ + ( "a" ) ⃗ – ( "d" ) ⃗ = 0 proved.


Example 6: If ( "a" ) ⃗ = 2( "i" ) ⃗ – 4( "j" ) ⃗ and ( "b" ) ⃗ = –3( "i" ) ⃗ + 2( "j" ) ⃗, find the vector ( "c" ) ⃗ such that 2( "a" ) ⃗ – ( "b" ) ⃗ + 3( "c" ) ⃗ = 0. Solution: Here, ( "a" ) ⃗ = 2( "i" ) ⃗ – 4( "j" ) ⃗ and ( "b" ) ⃗ = –3( "i" ) ⃗ + 2( "j" ) ⃗ Given, 2( "a" ) ⃗ – ( "b" ) ⃗ + 3( "c" ) ⃗ = 0 i.e. 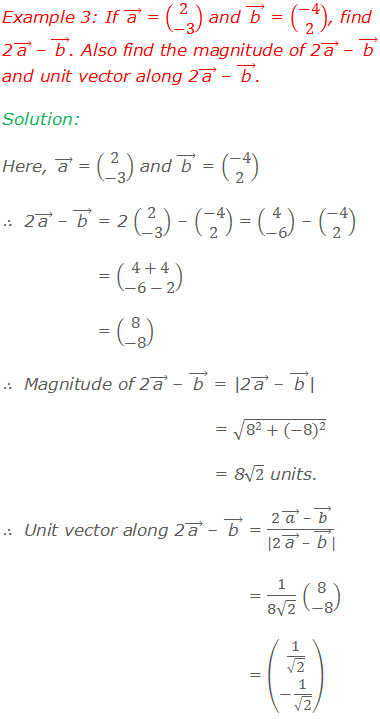2(2( "i" ) ⃗ – 4( "j" ) ⃗) – (–3( "i" ) ⃗ + 2( "j" ) ⃗) + 3( "c" ) ⃗ = 0 or, 4( "i" ) ⃗ – 8( "j" ) ⃗ + 3( "i" ) ⃗ – 2( "j" ) ⃗ + 3( "c" ) ⃗ = 0 or, 7( "i" ) ⃗ – 10( "j" ) ⃗ + 3( "c" ) ⃗ = 0 or, 3( "c" ) ⃗ = –7( "i" ) ⃗ + 10( "j" ) ⃗ ∴ ( "c" ) ⃗ = – 7/3 ( "i" ) ⃗ + 10/3 ( "j" ) ⃗


Example 7: PQRSTU is a regular hexagon, show ("PR" ) ⃗ + ("PS" ) ⃗ + ("UP" ) ⃗ + ("TP" ) ⃗ = 3("PQ" ) ⃗. Solution: Here, PQRSTU is a regular hexagon. Join UR. Then by the property of regular hexagon, 2("PQ" ) ⃗ = ("UR" ) ⃗. Now, from ΔPRU, ("UP" ) ⃗ + ("PR" ) ⃗ = ("UR" ) ⃗ Again, from ΔPST, ("TP" ) ⃗ + ("PS" ) ⃗ = ("TS" ) ⃗ ∴ ("PR" ) ⃗ + ("PS" ) ⃗ + ("UP" ) ⃗ + ("TP" ) ⃗ = (("UP" ) ⃗ + ("PR" ) ⃗) + (("TP" ) ⃗ + ("PS" ) ⃗) = ("UR" ) ⃗ + ("TS" ) ⃗ = 2("PQ" ) ⃗ + ("PQ" ) ⃗ [∵ ("TS" ) ⃗ = ("PQ" ) ⃗] = 3("PQ" ) ⃗ Hence, ("PR" ) ⃗ + ("PS" ) ⃗ + ("UP" ) ⃗ + ("TP" ) ⃗ = 3("PQ" ) ⃗. Proved.

Do you have any questions regarding the vector operations?


You can ask your questions or problems here, in the comment section below.

Labels:

0 comments:

Subscribe to: Post Comments (Atom)