Ogive (Cumulative frequency curve)

Ogive (Cumulative frequency curve)

 

Ogive is a graphical representation of the cumulative frequency distribution of continuous series.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

In a continuous series, if the upper limit (or the lower limit) of each class interval is taken as x-coordinate and its corresponding cumulative frequency (c.f.) as y-coordinate and the points are plotted in the graph, we obtain a curve by joining the points with freehand. Such a curve is known as the ogive or cumulative frequency curve. It is also called a free hand curve.

 

Since less than c.f. and more than c.f. are the two types of cumulative frequencies, there are two types of ogives as well. They are:

 

1.   Less than ogive (or less than cumulative frequency curve)

2.   More than ogive (or more than cumulative frequency curve)

Less than ogive

 

When the upper limit of each class interval is taken as x-coordinate and its corresponding frequency as y-coordinate, the ogive so obtained is known as less than ogive (or less than cumulative frequency curve).

 

Obviously, less than ogive is an increasing curve, sloping upwards from left to right and has the shape of an elongated S.

 

Construction of less than ogive:

 

To construct a less than ogive, we proceed through the following steps:

 

1.   Make a less than cumulative frequency table.

2.   Choose the suitable scale and make the upper class limit of each class interval along the x-axis and cumulative frequencies along the y-axis.

3.   Plot the coordinates (upper limit, less than c.f.) on the graph.

4.   Join the points by freehand and obtain a less than ogive.

  

More than ogive

When the lower limit of each class interval is taken as x-coordinate and its corresponding frequency as y-coordinate, the ogive so obtained is known as more than ogive (or more than cumulative frequency curve).

 

More than ogive is a decreasing curve sloping downward from left to right and has the shape of an elongated S, upside down.

 

 

Construction of less than ogive:

 

To construct a more than ogive, we proceed through the following steps:

 

1.   Make a more than cumulative frequency table.

2.   Choose the suitable scale and make the lower class limit of each class interval along the x-axis and cumulative frequencies along the y-axis.

3.   Plot the coordinates (lower limit, more than c.f.) on the graph.

4.   Join the points by freehand and obtain a more than ogive.

Examples:

 

Example 1: The table given below shows the marks obtained by 80 students in science. Construct (i) less than ogive  (ii) more than ogive.

Solution: Here,

 

Less than cumulative frequency distribution table:

Here, we have the coordinates to draw less than ogive: (10, 3), (20, 11), (30, 28), (40, 57), (50, 72), (60, 78) and (70, 80).

 

Plotting these points on a graph, we have the following less than ogive.

 

More than cumulative frequency distribution table:

Here, we have the coordinates to draw more than ogive: (0, 80), (10, 77), (20, 69), (30, 52), (40, 23), (50, 8) and (60, 2).

Plotting these points on a graph, we have the following more than ogive.

 

 

 

Less than and more than (Combined) Ogive

 

If we draw both less than and more than ogive of a distribution on the same graph paper, it is called combined ogive. The point of intersection of two ogives in a combined ogive is called the vital-point. 

The foot of the perpendicular drawn from vital-point to x-axis gives the value of the median of the distribution. And, the corresponding class is the proper class for the median.

Uses of ogive

 

Following are the uses of cumulative frequency curve (ogive):

 

1. Ogive or cumulative frequency curve helps us to determine as well as portray the number or proportion of cases above or below the given value.

2. Median (Q₂) and quartiles i.e. lower quartile (Q₁) and upper quartile (Q₃) can be estimated from the ogive of a frequency distribution.

 

Examples:

 

Example 2: Construct the combined ogive from the data given in the table of Example 1, and find the median.

 

Solution: Here,

 

Less than and more than cumulative frequency distribution table:

Here, we have the coordinates to draw less than ogive: (10, 3), (20, 11), (30, 28), (40, 57), (50, 72), (60, 78) and (70, 80).

 

Here, we have the coordinates to draw more than ogive: (0, 80), (10, 77), (20, 69), (30, 52), (40, 23), (50, 8) and (60, 2).

 

Plotting these points on a graph, we have the following less than and more than combined ogive.

 

 

A perpendicular is drawn from the point of intersection of two ogives which meets the x-axis at 34.14 (approx.) units from the origin. So, the required median of the given distribution is 34.14.

Example 3: The table given below shows the marks obtained by 60 students in mathematics. Construct a less than ogive and compute median, first quartile (Q₁) and third quartile (Q₃).

Solution: Here,

 

Less than cumulative frequency distribution table,

Here, we have the coordinates to draw less than ogive: (10, 4), (20, 14), (30, 34), (40, 49), (50, 55) and (60, 60).

 

Plotting these points on a graph, we have the following less than ogive.

 

 

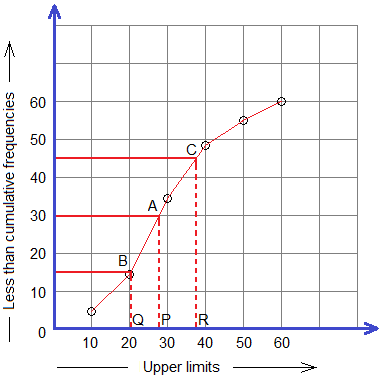
Median lies in 50% of the total data.

∴ 50% of 60 students = 30 students

Q₁ lies in 25% of the total data.

∴ 25% of 60 students = 15 students

Q₃ lies in 75% of the total data.

∴ 75% of 60 students = 45 students

 

Straight lines drawn from 30, 15, and 45 (frequency) on y-axis parallel to x-axis intersects the curve at A, B, and C. And, perpendiculars drawn from A, B, and C meets the x-axis at P, Q, and R with x-coordinates 28, 20.5, and 37.33 respectively.

 

Therefore,

 

Median = 28 (approx.)

Q₁ = 20.5 (approx.)

Q₃ = 37.33 (approx.) 

Example 4: Draw the less than ogive from the following data and the questions.

a. Find the no. of workers having wages more than 40.

b. Find the no. of workers having wages less than 80.

c. Find the no. of workers having wages between 80 and 100.

Solution: Here,

 

Less than cumulative frequency distribution table,

Here, we have the coordinates to draw less than ogive: (20, 5), (40, 13), (60, 23), (80, 32) and (100, 35).

 

Plotting these points on a graph, we have the following less than ogive.

 

 

From the graph,

 

a. No. of workers having wages more than 40 = (35 – 13) = 22

b. No. of workers having wages less than 80 = 32

c. No. of workers having wages between 80 and 100 = 3

Example 5: From the given cumulative frequency curve (ogive), determine the lower quartile (Q₁) class, median (Q₂) class and upper quartile (Q₃) class.

Solution: From the given graph,

 

Total number of data (N) = 40

 

Passing the lines from 10, 20, and 30 of the y-axis (i.e cumulative frequencies) parallel to x-axis, we get the corresponding points on the ogive curve. And, again vertical lines from those points give the required class for Q₁, Q₂ and Q₃.

Therefore, from the above graph, 

∴ Q₁ class = 10-20

∴ Q₂ class = 30-40

∴ Q₃ class = 40-50

Do you have any questions regarding the ogive?

 

You can ask your questions or problems here, in the comment section below.