Quartiles

8 comments
Quartiles



Quartiles

 

Quartiles are the values that divide the data arranged in ascending or descending order into four equal parts. A distribution can be divided into four equal parts by three quartiles.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver



********************


Install 10 Math Problems




********************



-      The first or lower quartile (Q1) is the point below which 25% of the items lie and above which 75% of the items lie.

-      The second quartile (Q2) is the point below which 50% of the items lie and above which 50% of the items lie. Of course, the second quartile is the median.

-      The third or upper quartile (Q3) is the point below which 75% of the items lie and above which, 25% of the items lie.

 

If N is the number of items in a distribution (data) arranged in ascending or descending order, then

 

In the case of the individual and discrete data,


First quartile (Q1) = (("N" +"1" )/"4" )^"th" item Second quartile (Q2) = (("N" +"1" )/"2" )^"th" item Third quartile (Q3) = ("3" 〖"(N" +"1)" 〗^"th" )/"4" item


In case of the grouped or continuous data,


First quartile (Q1) = L + " i " /"f" ("N" /"4" -"cf" ) Second quartile (Q2) = L + " i " /"f" ("N" /"2" -"cf" ) Third quartile (Q3) = L + " i " /"f" ("3N" /"4" -"cf" )

Where,

L = lower limit of the quartile class

f = frequency of the quartile class

cf = cumulative frequency of preceding class

i = height of class-interval

 

 

Worked Out Examples

 

Example 1: Calculate the quartiles from the data: 4, 6, 5, 9, 8, 10, 3

 

Solution: Here,

Data in ascending order: 3, 4, 5, 6, 8, 9, 10

No. of data (N) = 7

∴ first quartile (Q1) = (("N" +"1" )/"4" )^"th" item = (("7" +"1" )/"4" )^"th" item = ("8" /"4" )^"th" item = 2nd item = 4 ∴ 2nd quartile (Q2) = (("N" +"1" )/"2" )^"th" item = (("7" +"1" )/"2" )^"th" item = ("8" /"2" )^"th" item = 4th item = 6 ∴ 3rd quartile (Q3) = ("3" 〖"(7" +"1)" 〗^"th" )/"4" item = ("3" 〖×"8" 〗^"th" )/"4" item = 6th item = 9

∴ Q1 = 4, Q2 = 6, and Q3 = 9 Ans.


Example 2: Calculate the quartiles from the data: 5, 8, 10, 11, 12, 14, 16, 18, 20, 4

 

Solution: Here,

Data in ascending order: 4, 5, 8, 10, 11, 12, 14, 16, 18, 20

No. of data (N) = 10

∴ first quartile (Q1) = (("N" +"1" )/"4" )^"th" item = (("10" +"1" )/"4" )^"th" item = ("11" /"4" )^"th" item = 2.75th item = 2nd + 0.75 (3rd – 2nd) items = 5 + 0.75 (8 – 5) = 5 + 2.25 = 7.25 ∴ 2nd quartile (Q2) = (("10" +"1" )/"2" )^"th" item = ("11" /"2" )^"th" item = 5.5th item = 5th + 0.5 (6th – 5th) items = 11 + 0.5 (12 – 11) = 11 + 0.5 = 11.5 ∴ 3rd quartile (Q3) = ("3" 〖"(N" +"1)" 〗^"th" )/"4" item = ("3" 〖"(10" +"1)" 〗^"th" )/"4" item = ("3" 〖×"11" 〗^"th" )/"4" item = ("33" /"4" )^"th" item = 8.25th item = 8th item + 0.25 (9th – 8th) items = 16 + 0.25 (18 – 16) = 16 + 0.5 = 16.5

∴ Q1 = 7.25, Q2 = 11.5, and Q3 = 16.5 Ans.


Example 3: Compute Q1 and Q3 from the following data.

Example 3 Table of data

Solution: Here, 

Frequency distribution table,

Solution 3: Frequency distribution table

Total number of data (N) = 17

∴ first quartile (Q1) = (("N" +"1" )/"4" )^"th" item = (("17" +"1" )/"4" )^"th" item = ("18" /"4" )^"th" item = 4.5th item = 20 ∴ 3rd quartile (Q3) = ("3" 〖"(7" +"1)" 〗^"th" )/"4" item = ("3" 〖"(17" +"1)" 〗^"th" )/"4" item = ("3" 〖×"18" 〗^"th" )/"4" item = 13.5th item = 35

∴ Q1 = 20 and Q3 = 35 Ans.


Example 4: Compute Q1 and Q3 from the following data.

Example 4: Table of data

Solution: Here, 

Frequency distribution table,

Solution 4: Frequency distribution table

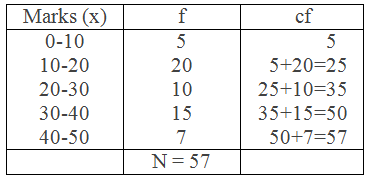
Here, N = 57

Q1 class = ("N" /"4" )^"th" class = ("57" /"4" )^"th" class = 14.25th class = 10-20 ∴ L= 10, f = 20, cf = 5, i= 10 ∴ Q1 = L + " i " /"f" ("N" /"4" -"cf" ) = 10 + "10" /"20" (14.25 – 5) = 10 + 4.62 = 14.62 Q3 class = ("3N" /"4" )^"th" class = (("3" ×"57" )/"4" )^"th" class = 42.75th class = 30-40 ∴ L= 30, f = 15, cf = 35, i= 10 ∴ Q3 = L + " i " /"f" ("3N" /"4" -"cf" ) = 30 + "10" /"15" (42.75 – 35) = 30 + 5.16 = 35.16

∴ Q1 = 14.62 and Q3 = 35.16 Ans.

 

 

If you have any questions or problems regarding the Quartiles, you can ask here, in the comment section below.


Was this article helpful? LIKE and SHARE with your friends…


Labels:

About author: Min Rajbanshi

I am a school math teacher and a blogger since 2012. I do blogging on a variety of topics including math. Over the years, I've explored and written about a wide range of topics, with a particular emphasis on mathematics. My passion for education extends beyond the classroom, as I enjoy sharing knowledge and insights on various subjects through my blog.

8 comments:

  1. UnknownJuly 31, 2021 at 4:23 AM

    Practical use of Quartile in real life?

    ReplyDelete
    Replies
    1. Min RajbanshiJuly 31, 2021 at 9:08 AM

      Quartiles and IQR (Inter Quartile Range) are used by companies to benchmark ourselves and the other companies. For example, the pay scale for a certain position is determined on the basis of the benchmark of the company which is measured on the basis of quartiles of different data related to the company.

      It is also used for the measure of sells and traffic of any product, website, web application, software, mobile app etc.

      Delete
  2. Luis MillonsOctober 27, 2021 at 1:41 PM

    Hello :D! I have a question, why in the final exercise Q3 you wrote 10/15?, just that thank you.

    ReplyDelete
  3. UnknownFebruary 24, 2022 at 6:39 AM

    in example 4
    how we know valus of cf,L and i

    ReplyDelete
    Replies
    1. Min RajbanshiFebruary 24, 2022 at 6:50 AM

      After finding the quartile class,

      L = lower limit of the quartile class
      f = frequency of the quartile class
      cf = cumulative frequency of preceding class
      i = height of class-interval

      Delete
    2. UnknownMay 27, 2023 at 10:29 PM

      If i is the height of class interval then, it must be 11 instead of 10.

      Delete
  4. UnknownApril 9, 2022 at 6:37 AM

    Shouldn't it be the last intervel in the last question

    ReplyDelete

Subscribe to: Post Comments (Atom)