
Every rational number or fraction can
be expressed in terms of decimal numbers by the actual division. And, those
decimal numbers can either be terminating or non-terminating.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
What are terminating decimals?
Terminating decimal is a fraction decimal having a finite number of digits after decimal point. In this case division ends after a finite number of stages. For example : 1/5, 1/4, 1/8 etc. are terminating decimals because,

What are non-terminating decimals?
Non-terminating decimal is a fraction decimal having infinite number of digits after decimal point. In this case division never ends but recur the same digit or group of digits again and again. So they are also called recurring decimals. For example: 1/3, 2/3, 4/7 etc. are non-terminating decimals because,

Here, a number or group of numbers are
repeated and do not end after a finite number of stages, such number are
denoted by a dot (.) or a bar(–) above it.

Types of Non-terminating Decimals:
There are two types of non-terminating (recurring) decimals:
a.
Simple recurring decimals: In this
case the recurring starts just after the decinal point. For example, 0.333…
b.
Mixed recurring decimals: In this
case the recurring does not start just after the decimal point. For example,
0.5181818…
Conversion of Decimal into Fraction
For terminating decimal we can convert a decimal into fraction simply by removing decimal and dividing by 10 if there is 1 decimal place, by 100 if there is 2 decimal places and by 1000 if there is 3 decimal places and so on. For example:

For non-terminating decimal we can convert a decimal into fraction by the following method as given in the example below:



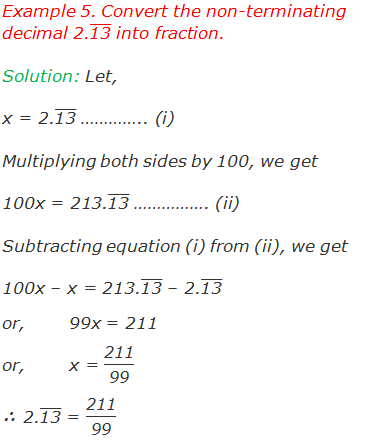
Do you have any questions regarding the Terminating and Non-terminating Decimals?
You can ask your questions or problems in the comment section below.



0 comments: