Surface Area of a Cone

Surface Area of a Cone

 

A cone is a pyramid with a circular base. A solid cone has two types of surfaces, one is the curved surface around the cone and another is the plane surface of its circular base.

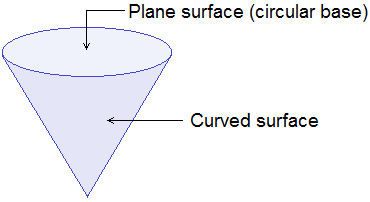
The surface area of a cone can be measured on the basis of its slant height and the radius of the base.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

The curved surface area of a cone is given by the formula πrl, where r is the radius and l is the slant height of the cone.

 

This formula can be derived by the following activity:

1.    Take a hollow right circular cone of vertical height h, radius r and slant height l.

2.    Cut this cone along the slant height and spread it out. The spread-out figure is a sector of a circle of radius l (slant height of the cone). The arc of this sector is equal to the circumference of the base of the cone.

3.    Divide the sector into many small parts as you can and arrange as shown in the figure.

In this way, we can get a rectangle of length l and breadth πr as shown in the figure.

Now,

The Curved Surface Area (CSA) of the cone, 

          = Area of the sector

          = Area of rectangle

          = length × breadth

          = l × πr

          = πrl

 

∴   Curved Surface Area (CSA) of the cone = πrl

 

And, 

The Total Surface Area (TSA) of the cone, 

          = Curved surface area + Area of circular base

          = πrl + πr²

          = πr (r + l)

 

∴   Total Surface Area (TSA) of a cone = πr (r + l).

 

 

Worked Out Examples

 

Example 1: Find the total surface area of a cone whose radius = 5 cm and height = 12 cm.

Solution:

Here,

Radius of cone (r) = 5 cm

Height (h) = 12 cm

Slant height (l) = √(h² + r²)

= √(12² + 5²)

= √(144 + 25)

= √169

= 13 cm

 

Now,

Total surface area of cone = πr (r + l)

                   = 22/7 × 5 (5 + 13)

                   = 22/7 × 5 × 18

                   = 282.85 cm²

 

∴ The total surface area of the cone is 282.85 cm². Ans.

Example 2: The circumference of the base of a tent is 17.6 m. The slant height is 3.5 m. Find the area of the canvas used for the tent.

 

Solution:

Here,

Circumference (c) = 17.6 m

i.e.    2πr = 17.6

or,     πr = 17.6/2

or,     πr = 8.8 m

 

Slant height (l) = 3.5 m

 

Now,

Area of canvas required 

          = Curved surface area of the cone

          = πrl

          = 8.8 × 3.5

          = 30.8 m²

 

∴ The area of canvas required is 30.8 m². Ans.

 

 

Example 3: A cone with a hemisphere on the top has a common radius of 21 cm. If the slant height of the cone is 75 cm, find the total surface area of the solid object.

Solution:

Here,

Common radius (r) = 21 cm

Slant height of the cone (l) = 75 cm

 

Now,

Total suface area of the solid (A) 

          = CSA of hemisphere + CSA of cone

          = 2πr² + πrl

          = πr (2r + l)

          = 22/7 × 21 (2×21 + 75)

          = 7722 cm²

 

Thus, the TSA of the given solid is 7722 cm².

 

 

If you have any questions or problems regarding the Surface Area of Cone, you can ask here, in the comment section below.

Was this article helpful? LIKE and SHARE with your friends…