Triangular Prism

Triangular Prism

 

A prism having triangular bases is called a triangular prism. A triangular prism has three rectangular faces (lateral surfaces) and two triangular faces (bases) as shown in the figure below.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Lateral Surface Area of Triangular Prism (LSA)

Let a, b, and c be the three sides of the triangular base, and h be the height of the prism. Lateral surface area of a triangular prism is the area of three rectangular faces (R₁, R₂ and R₃) of the prism as shown in the net of triangular prism in the figure given below.

 ∴ Lateral surface area (LSA)

                   = area of R₁ + R₂ + R₃

                   = ah + bh + ch

                   = (a + b + c)h

                   = perimeter of triangular base × height

                   = Ph

 

[∴ Lateral surface area (LSA) = Ph]

Total Surface Area of Triangular Prism (TSA)

Total surface area of a triangular prism is the sum of the lateral surface area and the areas of two triangular bases.

 

∴ Total surface area (TSA)

                   = LSA + 2 × area of triangular base

                   = Ph + 2A

 

[∴ Total surface area (TSA) = Ph + 2A]

 

 

The volume of the Triangular Prism (V)

 

The volume of a triangular prism is the total space occupied by the prism. It is given by the product of its area of the base and the height of the prism.

 

i.e. Volume of the triangular prism(V),

          = Area of triangular base × height of the prism

          = A × h

 

[∴ Volume of the triangular prism (V) = Ah]

Worked Out Examples

Example 1: Find the lateral surface area, total surface area, and volume of the given triangular prism.

Solution:

 

Here,

 

Base of the prism is a right-angled triangle,

        AB = 6cm

        BC = 8cm

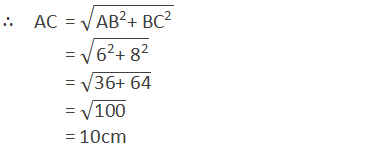
∴  Perimeter of base (P) = 6 + 8 + 10 =24cm

 

∴  Area of triangular base (A) = ½ AB × BC

= ½ × 6 × 8

= 24cm²

 

Height of prism (h) = 20cm

 

∴  Lateral surface area (LSA) = P × h

                               = 24cm × 20cm

                               = 480cm²

 

∴  Toral surface area (TSA) = LSA + 2A

                            = 480 + 2 × 24

                            = 480 + 48

                            = 528cm²

 

∴  Volume (V) = A × h

                   = 24cm² × 20cm

                   = 480cm³ 

∴  LSA = 480 cm², TSA = 528 cm² and Volume = 480 cm³  Ans.

Example 2: Find the lateral surface area, total surface area, and volume of the given triangular prism.

Solution:

 

Here,

 

Base of prism is equilateral triangle of length (a) = 6cm

 

∴  Perimeter of base (P) = 6 + 6 + 6 =18cm

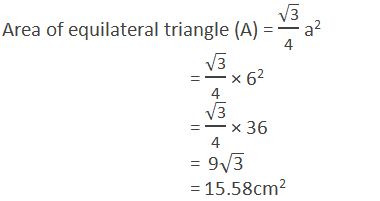
Height of prism (h) = 15cm

 

∴  Lateral surface area (LSA) = P × h

                               = 18cm × 15cm

                               = 270cm²

 

∴  Toral surface area (TSA) = LSA + 2A

                            = 270 + 2 × 15.58

                            = 270 + 31.16

                            = 301.16cm²

 

∴  Volume (V) = A × h

                   = 15.58cm² × 15cm

                   = 233.7cm³ 

∴  LSA = 270 cm², TSA = 301.15 cm² and Volume = 233.7 cm³  Ans.

Example 3: Find the lateral surface area, total surface area, and volume of the given triangular prism.

 

Solution:

 

Here,

 

Three sides of base triangle are,

a = 13cm

b = 14cm

c = 15cm

 

∴  Perimeter of base (P) = 13 + 14 + 15 = 42cm

 

∴  Semi-perimeter (s) = 42/2 = 21cm

Height of prism (h) = 20cm

 

∴  Lateral surface area (LSA) = P × h

                               = 42cm × 20cm

                               = 840cm²

 

∴  Toral surface area (TSA) = LSA + 2A

                            = 840 + 2 × 84

                            = 840 + 168

                            = 1008cm²

 

∴  Volume (V) = A × h

                   = 84cm² × 20cm

                   = 1680cm³

∴  LSA = 840 cm², TSA = 1008 cm² and Volume = 1680 cm³  Ans. 

If you have any question or problems regarding the Triangular Prism, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…