
Area of Quadrilateral
Area is the region covered by a closed plane figure.
Quadrilateral is a closed plane figure bounded by four sides. Area of
quadrilaterals can be measured by using different formula for different types
of regular shaped quadrilaterals. They are as given below:
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Area of rectangle = l × b,
where l = length of rectangle and b = breadth of rectangle
Area of square = l2 or ½ d2, where l = length of square and d =
diagonal
Area of parallelogram = b × h, where b = base and h = height
Area of rhombus = ½ × d1 × d2, where d1 and d2 are
two diagonals
Area of kite = ½ × d1 × d2, where d1 and d2 are
two diagonals
Area of trapezium = ½ × h × (l1 + l2), where h = height and l1 and l2
are two parallel lines
Area of a irregular quadrilateral
Area of irregular or any shaped quadrilateral can be
obtained in terms of its one diagonal and two perpendiculars drawn from the
opposite vertices to the diagonal.
In the given figure, PQRS is a quadrilateral in which QS is a diagonal. PA and RB are perpendiculars drawn from the vertex P and R respectively to the
diagonal QS. Suppose, QS = d, PA = h1 and RB = h2.
We can write:
Area of quadrilateral PQRS = Area of ΔPQS + Area of ΔRQS
= ½ QS × PA + ½ QS × RB
= ½ d ×h1 + ½ d × h2
= ½ d (h1 + h2)
∴
Area of quadrilateral = ½ d (h1 + h2) where, d is a diagonal, h1 and h2 are the perpendiculars drawn from the opposite vertices to the diagonal d.
Workout Example
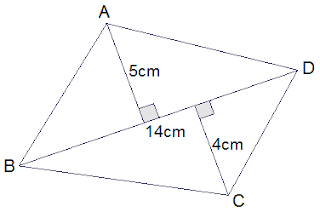
Example 1: Find the area of the given
quadrilateral.
Solution:
From the figure,
Length
of diagonal (d) = 14cm
h1
= 5cm
h2
= 4cm
Area
of quadrilateral = ½ d (h1 + h2)
= ½ × 14 (5 + 4)
= ½ × 14 × 9
= 63 cm2
You can comment your questions or problems regarding the area of quadrilaterals here.





0 comments: