Factors of 50

 

The factors of 50 are 1, 2, 5, 10, 25, and 50 i.e. F₅₀ = {1, 2, 5, 10, 25, 50}. The factors of 50 are all the numbers that can divide 50 without leaving a remainder.

 

We can check if these numbers are factors of 50 by dividing 50 by each of them. If the result is a whole number, then the number is a factor of 50. Let's do this for each of the numbers listed above:

 

·        1 is a factor of 50 because 50 divided by 1 is 50.

·        2 is a factor of 50 because 50 divided by 2 is 25.

·        5 is a factor of 50 because 50 divided by 5 is 10.

·        10 is a factor of 50 because 50 divided by 10 is 5.

·        25 is a factor of 50 because 50 divided by 25 is 2.

·        50 is a factor of 50 because 50 divided by 50 is 1.

 

 

How to Find Factors of 50?

 

1 and the number itself are the factors of every number. So, 1 and 50 are two factors of 50. To find the other factors of 50, we can start by dividing 50 by the numbers between 1 and 50. If we divide 50 by 2, we get a remainder of 0. Therefore, 2 is a factor of 50. If we divide 50 by 3, we get a remainder of 2. Therefore, 3 is not a factor of 50.

 

Next, we can check if 4 is a factor of 50. If we divide 50 by 4, we get a remainder of 2. Therefore, 4 is not a factor of 50. We can continue this process for all the possible factors of 50.

 

Through this process, we can find that the factors of 50 are 1, 2, 5, 10, 25, and 50. These are the only numbers that can divide 50 without leaving a remainder.

 

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Properties of the Factors of 50

 

The factors of 50 have some interesting properties. One of the properties is that the sum of the factors of 50 is equal to 93. We can see this by adding all the factors of 50 together:

 

1 + 2 + 5 + 10 + 25 + 50 = 93

 

Another property of the factors of 50 is that the prime factors of 50 are 2, and 5 only.

 

 

Applications of the Factors of 50

 

The factors of 50 have several applications in mathematics. One of the applications is in finding the highest common factor (HCF) of two or more numbers. The HCF is the largest factor that two or more numbers have in common. For example, to find the HCF of 50 and 60, we need to find the factors of both numbers and identify the largest factor they have in common. The factors of 50 are 1, 2, 5, 10, 25, and 50. The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. The largest factor that they have in common is 10. Therefore, the HCF of 50 and 60 is 10.

 

Another application of the factors of 50 is in prime factorization. Prime factorization is the process of expressing a number as the product of its prime factors. The prime factors of 50 are 2, and 5 since these are the only prime numbers that can divide 50 without leaving a remainder. Therefore, we can express 50 as:

 

50 = 2 × 5 × 5

 

We can do prime factorization by division and factor tree method also. Here is the prime factorization of 50 by division method,

 

∴ 50 = 2 × 5 × 5

 

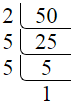
Here is the prime factorization of 50 by the factor tree method,

 

∴ 50 = 2 × 5 × 5

 

 

Conclusion

 

The factors of 50 are the numbers that can divide 50 without leaving a remainder. The factors of 50 are 1, 2, 5, 10, 25, and 50. The factors of 50 have some interesting properties, such as having a sum of 93. The factors of 50 have several applications in mathematics, such as finding the highest common factor and prime factorization.