Sum of Arithmetic Series

Arithmetic Series

 

The series associated with an arithmetic sequence is known as an arithmetic series. For example: 3 + 7 + 11 + 15 + 19 + 23 + 27 + 31 is the arithmetic series associated with the arithmetic sequence: 3, 7, 11, 15, 19, 23, 27, 31.

 

Sum of Arithmetic Series

 

To derive the formula for the sum of arithmetic series, let us suppose an arithmetic series where a be the first term, d be the common difference, n be the number of terms, l be the last term and S_n be the sum of the n terms of an arithmetic series (AS), then,

S_n = a + (a + d) + (a + 2d) + … … … + (l – 2d) + (l – d) + l ………… (i)

 

Writing in the reverse order, we have,

S_n = l + (l – d) + (l – 2d) + … … … + (a + 2d) + (a + d) + a ………… (ii)

 

Adding relations (i) and (ii), we get

2S_n = (a + l) + (a + l) + (a + l) + … … … + (a + l) + (a + l) + (a + l).

or, 2S_n = n(a + l)

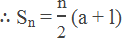
Again, the last term, l = a + (n – 1)d

Therefore, the sum of the arithmetic series can be found by using the following formulas:

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Worked Out Examples

 

Example 1: Find the sum of the series 2 + 8 + 14 + 20 + … … … 20 terms.

 

Solution:

 

Here,

First term (a) = 2

Common difference (d) = 8 – 2 = 6

Number of terms (n) = 20

Sum (S_n) = ?

 

We Know,

 

Solution:

 

Here,

First term (a) = 22 

Last term (l) = 54

Number of terms (n) = ?

Sum (S_n) = ?

 

We know,

l = a + (n – 1)d

or, n – 1 = 6

∴ n = 7

 

Now,

 

Hence, the required sum is 266.

 

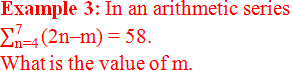
Solution:

 

Given,

or, (3×4 – m)+ (3×5 – m)+ (3×6 – m)+ (3×7 – m) = 58

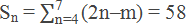
or, (12 – m)+ (15 – m)+ (18 – m)+ (21 – m) = 58

or, 12 – m + 15 – m + 18 – m + 21 – m = 58

or, 66 – 4m = 58

or, 4m = 66 – 58

or, 4m = 8

 

∴ m = 2

 

Solution:

 

Given,

 

Example 5: How many terms of an AS 17 + 15 + 13 + … … are needed to give the sum 80?

 

Solution:

 

Here,

First term (a) = 17

Common difference (d) = -2

Sum (S_n) = 80

Number of terms (n) = ?

 

By using formula,

or, 160 = n[34 – 2n + 2]

or, 2n² – 36n + 160 = 0

or, n² – 18n + 80 = 0

or, n² – 10n – 8n + 80 = 0

or, (n – 10)(n – 8) = 0

∴ n = 8 or 10

 

 

Example 6: If the sum of the first 16 terms of an AS is 280 and the 6^th term of the series is 14. Find the sum of the first 21 terms.

 

Solution:

 

Let a be the first term and d be the common difference of the given series.

Sum of 16 terms (S₁₆) = 280

6^th term (t6) = 14

 

By using formula, we have

or, 280 = 8(2a + 15d)

or, 2a + 15d = 35 …………… (i)

 

Again,

t_n = a + (n – 1)d

or, t₄ = a + (6 – 1)d

or, a + 5d = 14 …………… (ii)

 

Solving equations (i) and (ii), we get

Substituting the value in equation (ii),

a + 5 × 7/5 = 14

or, a + 7 = 14

or, a = 7

 

Now,

or, S₂₁ = 441

 

Hence, the sum of 21 terms of the series is 441.

 

 

Example 7: Find the sum of all natural numbers less than 100 which are exactly divisible by 7.

 

Solution:

 

Here,

 

First term (a) = 7

Common difference (d) = 7

Last term (l) =98

Sum (S_n) = ?

Number of terms (n) = ?

 

By using formula,

l = a + (n – 1)d

or, 98 = 7 + (n – 1)7

or, 98 = 7 + 7n – 7

or, 7n = 98

or, n = 14

 

Hence by using formula,

or, S₁₄ = 7 × 105

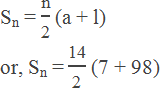
∴ S₁₄ = 735

 

∴ The required sum is 735.

 

 

Sum of the First n Natural Numbers

 

The first n natural numbers are 1, 2, 3, 4, … … … n.

Let S_n = 1 + 2 + 3 … … … + n

 

Here,

First term (a) = 1

Common difference (d) = 2 – 1 = 1

Number of terms (n) = n

Sum of first n terms (S_n) = ?

 

By using formula,

 

Sum of the First n Odd Natural Numbers

 

The first n odd natural number are 1, 3, 5, … … …, (2n – 1)

Let S_n = 1 + 3 + 5 + … … + (2n – 1)

 

Here,

First term (a) = 1

Common difference (d) = 3 – 1 = 2

Number of terms (n) = n

Sum of n terms (S_n) = ?

 

By using formula,

 

The Sum of the First n Even Natural Numbers

 

The first n even natural numbers are 2, 4, 6, … …, 2n.

Let S_n = 2 + 4 + 6 + … … + 2n

 

Here,

First term (a) = 2

Common difference (d) = 4 – 2 = 2

Number of terms (n) = n

Sum of n terms (S_n) = ?

 

By using formula,

 

Sum of the Squares of the First n Natural Numbers

 

The squares of the first n natural numbers are 1², 2², 3², … …, n²

Let S_n = 1² + 2² + 3² + … … + n²

 

Consider the identity,

r³ – (r – 1)³ = r³ – (r³ – 3r² + 3r – 1)

or, r³ – (r – 1)³ = 3r² – 3r + 1

Putting r = 1, 2, 3, 4, … …, (n – 1), n

1³ – 0³ = 3.1² – 3.1 + 1

2³ – 1³ = 3.2² – 3.2 + 1

3³ – 2³ = 3.3² – 3.3 + 1

4³ – 3³ = 3.4² – 3.4 + 1

… … … … … … … …

(n – 1)³ – (n – 2)³ = 3(n – 1)² – 3(n – 1) + 1

n³ – (n – 1)³ = 3n² – 3n + 1

 

Adding above all identities, we have

n³ = 3(1² + 2² + 3² + … … + n²) – 3(1 + 2 + 3 + … … + n) + n

 

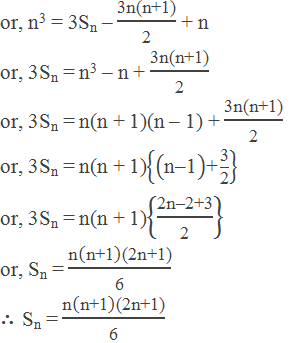
Sum of the Cubes of the First n Natural Numbers

 

The cubes of the first n natural numbers are 1³, 2³, 3³, … …, n³.

Let S_n = 1³ + 2³ + 3³ + … … + n³

 

Consider the identity,

k⁴ – (k – 1)⁴ = k⁴ – (k⁴ – 4k³ + 6k² – 4k + 1)

or, k⁴ – (k – 1)⁴ = 4k³ – 6k² + 4k – 1

Putting k = 1, 2, 3, 4, … …, (n – 1), n.

1⁴ – 0⁴ = 4.1³ – 6.1² + 4.1 – 1

2⁴ – 1⁴ = 4.2³ – 6.2² + 4.2 – 1

3⁴ – 2⁴ = 4.3³ – 6.3² + 4.3 – 1

4⁴ – 3⁴ = 4.4³ – 6.4² + 4.4 – 1

… … … … … … … … … …

(n – 1)⁴ – (n – 2)⁴ = 4.(n – 1)³ – 6.(n – 1)² + 4.(n – 1) – 1

n⁴ – (n – 1)⁴ = 4.n³ – 6.n² + 4.n – 1

 

Adding all above identities, we have,

n⁴ = 4(1³ + 2³ + 3³ + … … + n³) – 6(1² + 2² + 3² + … … + n²) + 4(1 + 2 + 3 + … … + n) – n

or, 4S_n = n⁴ + n + n(n + 1)(2n + 1) – 2n(n + 1)

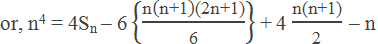
or, 4S_n = n(n + 1)(n² – n + 1) + n(n + 1)(2n + 1) – 2n(n + 1)

or, 4S_n = n(n + 1)(n² – n + 1 + 2n + 1 – 2)

 

More Examples

 

Example 8: Find the sum of the following series:

a. 2 + 4 + 6 + … … … 12 terms

b. 1³ + 2³ + 3³ + … … 10 terms

 

Solution:

 

a. The given series is 2 + 4 + 6 + … … … 12 terms

This is the sum of the first 12 even natural numbers.

 

Here, n = 12

∴ S_n = n(n + 1) = 12(12 + 1) = 156

 

b. The given series is 1³ + 2³ + 3³ + … … 10 terms

This is the sum of the cubes of the first 10 natural numbers

 

Here, n = 10

 

Example 9: The sum of three numbers in AP is 27 and the sum of their squares is 293. Find the numbers.

 

Solution:

 

Let the three numbers in AP be a – d, a and a + d.

Then,

(a – d) + a + (a + d) = 27

i.e. a = 9

 

And,

(a – d)² + a² + (a + d)² = 293

or, a² – 2ad + d² + a² + a² + 2ad + d² = 293

or, 3a² + 2d² = 293

or, 3 × 9² + 2d² = 293

or, d² = 25

or, d = 5

 

Hence, the required numbers are a – d, a and a + d.

i.e. 4, 9 and 14.

 

 

Example 10: Find n^th term and the sum of n terms of the series 2×3 + 3×4 + 4×5 + … … n terms.

 

Solution:

 

The given series is 2×3 + 3×4 + 4×5 + … … n terms.

n^th term of 2, 3, 4, … … = 2 + (n – 1)1 = n + 1

n^th term of 3, 4, 5, … … = 3 + (n – 1)1 = n + 2

The n^th term of the given series = (n + 1)(n + 2) = n² + 3n + 2

Sum of the series of n terms,