Arithmetic Mean (AM)

 

If three numbers a, b and c are in Arithmetic Sequence (AS) then the middle term b is said to be the arithmetic mean (AM) between the other two. For example, 10, 14 and 18 are in AS, so 14 is the arithmetic mean between 10 and 18. If any number of terms are in AS then the terms between the first and the last terms are known as the arithmetic means between the first and the last. For example, 11, 14, 17, 20, 23, 26, 29, 32 are in AS, so 14, 17, 20, 23, 26, 29 are the arithmetic means between 11 and 32.

 

Arithmetic Mean Between Two Numbers

 

Let M be the arithmetic mean between two numbers a and b, then a, M, b are in AS. Now by the definition of AS,

 

M – a = b – M

or, 2M = b + a

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Arithmetic Means Between Two Numbers

 

Let m₁, m₂, ………, m_n1 be the arithmetic means between a and b, then a, m₁, m₂, ………, m_n1, b are in AS.

 

If d be the common difference, then

t_n = a + (n – 1)d

 

As there are n₁ + 2 terms in all i.e. n = n₁ + 2

b = a + (n₁ + 2 – 1)d

or, b – a = (n₁ + 1)d

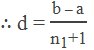
Now, the required arithmetic means are,

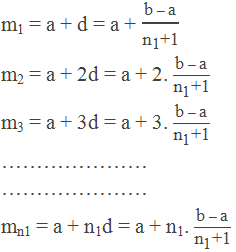
Note: The second term of the sequence is the first mean and the third term is the second mean and so on.

 

Worked Out Examples

 

Example 1: Find the arithmetic mean between 2 and 19.

 

Solution:

 

Here,

The first term (a) = 2

The last term (b) = 19

Arithmetic mean (AM) = ?

 

We know,

 

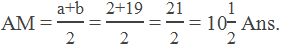
Example 2: If a, 30, b, 50, c are in AP, find the values of a, b and c.

 

Solution:

 

Here,

t₁ = a, t₂ = 30, t₃ = b, t₄ = 50, t₅ = c

 

Now,

Again,

Similarly,

Hence, values of a, b and c are 20, 40 and 60 respectively.

 

Example 3: If 10, m + 5, ………, 3m, 35 are the terms of AP. Find the value of m.

 

Solution:

 

Here,

First term (a) = 10 = t₁

Second term (t₂) = m + 5

Second last term (t_{n – 1}) = 3m

Last term (t_n) = 35

 

We know that,

t₂ – t₁ = t_n – t_{n – 1}

or, m + 5 – 10 = 35 – 3m

or, m – 5 = 35 – 3n

or, m + 3m = 35 + 5

or, 4m = 40

or, m = 10

 

Thus, the value of m = 10. Ans.

 

 

Example 4: If there are 6 AM between 4 and 11, then find the common difference.

 

Solution:

 

Here,

a = 4, b = 11 and number of means (n₁) = 6

 

We know,

∴ The common difference d = 1. Ans.

 

Example 5: Insert 5 arithmetic means between 2 and 18.

 

Solution:

 

Here,

The first term (a) = 2

The last term (b) = 18

No. of means (n₁) = 5

 

Hence, the common difference,

Hence, the required arithmetic means are,

 

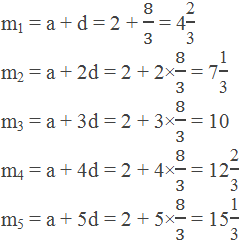
Example 6: There are n₁ arithmetic means between 12 and 33. If the fourth arithmetic mean is 24, find the value of n₁.

 

Solution:

 

Here,

The first term (a) = 12

The last term (b) = 33

The fourth mean (m₄) = 24

No. of means (n₁) = ?

 

We know,

Common difference,

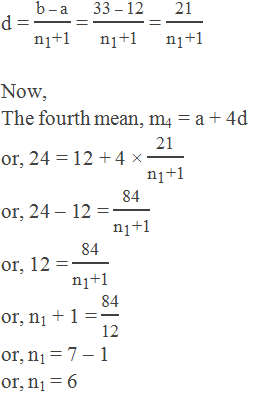
∴ n₁ = 6 Ans.

 

Example 7: There are n AM’s between 3 and 39. Find n so that the third mean : the last mean = 3:7.

 

Solution:

 

Here,

The first term (a) = 3

The last term (b) = 39

No. of means = n

Third mean : last mean (m₁:m₂) = 3:7

 

The common difference,

Now,

∴ n = 8 Ans.

 

 

Example 8: The product of two numbers is 375 and their arithmetic mean is 20, find the numbers.

 

Solution:

 

Let the numbers be a and b, the product of two numbers is 375

i.e. a × b = 375

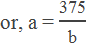
their AM is 20,

or, a + b = 20 × 2

or, a + b = 40

 

Now, putting the value of a from (i), we get

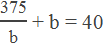
or, 375 + b² = 40b

or, b² – 40b + 375 = 0

or, b² – 25b – 15b + 375 = 0

or, b(b – 25) – 15(b – 25) = 0

or, (b – 25)(b – 15) = 0

 

∴ Either, b – 25 = 0 or, b = 25

Or, b – 15 = 0 or, b = 15

Hence, the required numbers are 15 and 25 or 25 and 15.

 

 

Example 9: One number is reciprocal to another and the arithmetic mean between them is 5/4. Find those numbers.

 

Solution:

 

Let one number be x then the other number be 1/x

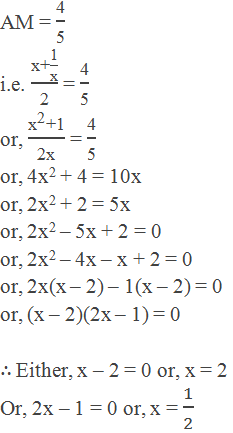
Hence, the required numbers are: