Inverse Function

 

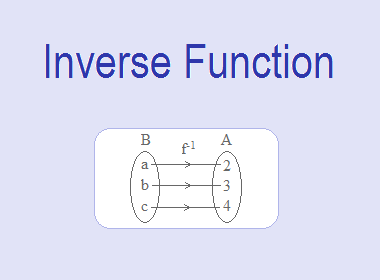
Let A = {2, 3, 4}, B = {a, b, c} and the function f : A → B is defined by f = {(2, a), (3, b), (4, c)}.

Here,

 

2 ∈ A, f(2) = a ∈ B

3 ∈ A, f(3) = b ∈ B

4 ∈ A, f(4) = c ∈ B

 

Also domain of f = {2, 3, 4} and range of f = {a, b, c}.

 

∴ f is one-to-one onto function.

 

Now we define a relation g : B → A so that g = {(a, 2), (b, 3), (c, 4)}.

Here,

 

a ∈ B, g(a) = 2

b ∈ B, g(b) = 3

c ∈ B, g(c) = 4

 

So, g is also one-to-one onto function.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

The function g is defined from B to A is said to be the inverse of f is denoted by f^-1. But for every function, there may not exist its inverse. Let us study the following examples.

 

1. f = {(2, 3), (3, 3), (4, 5)}.

Here, f is “many to one function.”

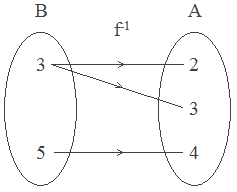
Here a relation from B to A is not a function as 3 ∈ B corresponds with more than one element of A. So, f^-1 does not exist.

 

 

2. f = {(2, 3), (4, 8), (5, 2)}.

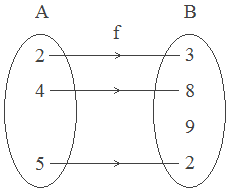
Here, f is a one-to-one into function.

Here, a relation from B to A is not a function because 9 ∈ B does not correspond with any element of A. So, f^-1 does not exist.

 

Hence, from the above examples, it is clear that to define an inverse function f must be a one-to-one onto function.

 

Definition of Inverse Function:

 

Let f : A → B be a one-to-one onto function. Then a function from B to A which associates each element of B with a unique element of A is called the inverse function of f. The inverse function from B to A is denoted by f^-1 : B → A.

 

 

Worked Out Examples:

 

Example 1: Let A = {a, b, c} and f : A → A is defined as f = {(a, c), (b, a), (c, b)}, find f^-1.

 

Solution:

 

Here,

 

f = {(a, c), (b, a), (c, b)}

 

Clearly, the function f is one-to-one onto, hence f^-1 exists and

f^-1 = {(c, a), (a, b), (b, c)}.

 

 

Example 2: Let f : R → R be defined by f(x) = 2x – 3, find the formula that defines f^-1.

 

Solution:

 

Here,

 

f : R → R and x is a variable, f is a one-to-one function, f^-1 exists.

 

y = f(x) = 2x – 3,

 

To find the inverse function we interchange the role of x and y,

 

i.e.  x = 2y – 3

or,  2y = x + 3

or,  y = (x + 3)/2

 

Hence, inverse function y = f^-1(x) = (x + 3)/2