Composite Function

 

Let A = {2, 3, 4}, B = {6, 9, 12} and C = {a, b, c}. If f : A → B and g : B → C are defined by f = {(2, 6), (3, 9), (4, 12)} and g = {(6, a), (9, b), (12, c)},

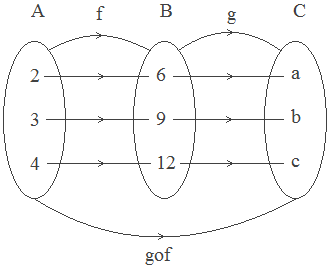
f is the function from A to B such that

 

2 ∈ A, f(2) = 6 ∈ B

3 ∈ A, f(3) = 9 ∈ B

4 ∈ A, f(4) = 12 ∈ B

 

Range of f = {6, 9, 12} = domain of g.

 

Again, g is the function from B to C such that

 

6 ∈ B, g(6) = a ∈ C

9 ∈ B, g(9) = b ∈ C

12 ∈ B, g(12) = c ∈ C

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Now, a function defined from A to C such that

 

2 ∈ A, a = g(6) = g(f(2)) ∈ C

3 ∈ A, b = g(9) = g(f(3)) ∈ C

4 ∈ A, c = g(12) = g(f(4)) ∈ C

 

Then this new function defined from set A to set C is said to be a composite function of f and g and is denoted by gof or simply gf. Hence, we have (gof)(2) = a, (gof)(3) = b, (gof)(4) = c.

 

Definition of Composite Function:

 

Let f : A → B and g : B → C be two functions. Then a new function defined from A to C such that every element of A corresponds with a unique element of C is known as the composite function of f and g. It is denoted by gof or simply gf.

 

Worked Out Examples:

 

Example 1: If f = {(2, 4), (6, 10), (8, 2)} and g = {(4, 6), (10, 2), (2, 6)}, then show that the function fog and gof in arrow diagram and find it in ordered pair form.

 

Solution:

 

Here,

 

For fog

fog(4) = f(g(4)) = f(6) = 10

fog(10) = f(g(10)) = f(2) = 4

fog(2) = f(g(2)) = f(6) = 10

 

Hence, fog = {(4, 10), (10, 4), (2, 10)}

 

For gof,

gof(2) = g(f(2)) = g(4) = 6

gof(6) = g(f(6)) = g(10) = 2

gof(8) = g(f(8)) = g(2) = 6

 

Hence, gof = {(2, 6), (6, 2), (8, 6)}

 

Example 2: If f : R → R and g : R → R be the two functions defined by f(x) = 3x + 7 and g(x) = 2(x – 8), find gof(x) and fog(x) and test whether gof(x) = fog(x) or not.

 

Solution:

 

Here,

 

f(x) = 3x + 7 and g(x) = 2(x – 8).

 

Now,

gof(x)         = g(f(x))

                   = g(3x + 7)

                   = 2{(3x + 7) – 8}

                   = 2 (3x – 1)

                   = 6x – 2

 

∴ gof(x) = 6x – 2

 

And,

 

fog(x)         = f(g(x))

= f(2(x – 8))

                   = f(2x – 16)

                   = 3(2x – 16) + 7

                   = 6x – 48 + 7

                   = 6x – 41

 

∴ fog(x) = 6x – 41

 

Hence, gof(x) ≠ fog(x)

 

 

Example 3: If f(x) = 2x – 1, g(x) = 3x and h(x) = x + 3, find

a. fogoh(x)

b. gofoh(2)

 

Solution:

 

Here,

 

We have, f(x) = 2x – 1, g(x) = 3x and h(x) = x + 3

 

a. fogoh(x) = f(goh(x))

                   = f(g(h(x)))

                   = f(g(x + 3))

                   = f(3(x + 3))

                   = f(3x + 9)

                   = 2(3x + 9) – 1

                   = 6x + 18 – 1

                   = 6x + 17

 

b. gofoh(2) = g(foh(2))

                   = g(f(h(2)))

                   = g(f(2 + 3))

                   = g(f(5))

                   = g(2 × 5 – 1)

                   = g(9)

                   = 3 × 9

                   = 27