Radian Measure (Circular System)

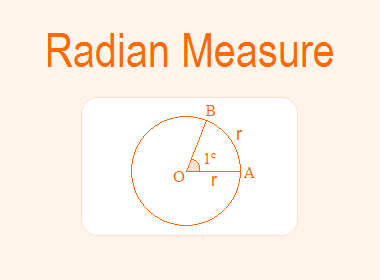
In the circular system of measurement of angles, the unit of angle is radian (^c). A radian, written as 1^c is the measure of an angle subtended at the centre of a circle by an arc equal to the length of its radius r.

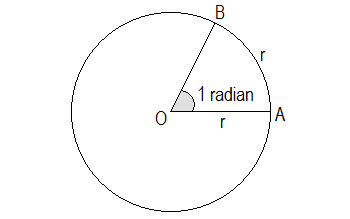
By measuring we can get the value of 1c = 57.27° nearly.

Note:

i.       ‘^c’ used in the notation of radian is the first letter of the word circular system.

ii.    When no unit is mentioned with an angle, it is always understood to be in radians.

 

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Prove that radian is a constant angle.

Proof:

Draw a circle with centre O and radius OA. Take any point B on the circumference such that arc AB is equal to the length of the radius OA. Join BO. Then ∠BOA = 1^c.

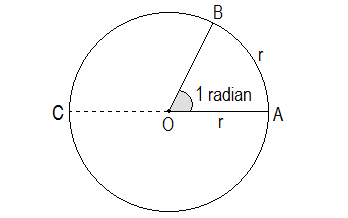
Produce AO to C such that CA is a diameter. Let OA = r = arc AB. Arc ABC = half of the circumference = 2πr/2 = πr

Now,

Central angles are proportional to their corresponding arcs.

Since 180° and π both are constant quantities. Hence, a radian is a constant angle.

 

Relation Among Degree, Grade and Radian Measures

The angle subtended at the centre of a circle by the total circular arc in radian measure is 2π radian (^c), in degree measure is 360 degree (°) and in grade measure is 400 grades (^g). It follows that,

2π radian = 360 degree (°) = 400 grades (^g)

i.e. π radian = 180 degree (°) = 400 grades (^g)

Using the above relation, we can convert degree, grade and radian to each other by using the approximate value of π as 22/7 or 3.1416.

 

Degrees to Radians

1 degree (°) = π/180 radians (^c)

∴ x degrees (°) = xπ/180 radians (^c)

 

Radians to Degrees

1 radian (^c) = 180/π degrees (°)

∴ x radians (^c) = x × 180/π degrees (°)

 

Grades to Radians

1 grade (^g) = π/200 radian (^c)

∴ x grades (^g) = x × π/200 radians (^c)

 

Radian to Grades

1 radian (^c) = 200/π grades (^g)

∴ x radians (^c) = x × 200/π grades (^g)

 

Worked Out Examples

Example 1: Express 75° into radian measures.

Solution: Here,

75° = 75 × π/180 radians = 5π/12 radians.

 

Example 2: Express 120g into radian measures.

Solution: Here,

120g = 120 × π/200 radians = 3π/5 radians.

 

Example 3: Express 3π/5 radian (^c) into degrees.

Solution: Here,

3π/5 radians = (3π/5) × (180/π) = 108 degree (°).

 

Example 4: Express 3π/5 radian (^c) into grades.

Solution: Here,

3π/5 radians = (3π/5) × (200/π) = 120 grades (^g).

 

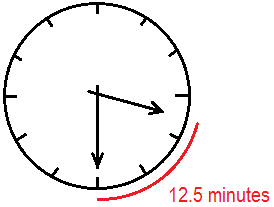
Example 5: Find the angle between minute hand and hour hand of a clock at 3:30 pm in radian.

Solution: At 3:30 pm, the distance between minute and hour hand in minute is 12.5 minutes.

Now,

     In 60 minutes, minute hand turns 360°

∴  In 1 minute, minute hand turns 360/60°

∴  In 12.5 minutes, min. hand turns 12.5 × 360/60°

                                      = 75°

                                      = 75 × π/180 radians

                                      = 5π/12 radians