Pythagorean theorem

 

Pythagoras (who died about 500 BC) was a Greek philosopher. He was a geometer and a great mystic, who with his followers, seems to have been the first to take mathematics seriously as a study in its own right as opposed to being a collection of formulae for practical calculation. The Pythagoreans are credited with the discovery of the well-known “Pythagoras Theorem” on right-angled triangles.

 

Right-angled Triangle and Its Components

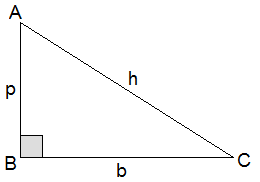
A triangle having one angle right angle i.e. 90° is called a right-angled triangle. In a right-angled triangle, the opposite side of the right angle is called the hypotenuse (h) and the other two sides are called the perpendicular (p) and the base (b). In the figure alongside, ∠B = 90°, AC is the hypotenuse (h), AB is the perpendicular (p) and BC is the base (b). In a right-angled triangle, the hypotenuse is the longest side.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

******************** 

 

Pythagorean Theorem

 

Pythagorean Theorem probably is the best-known theorem in geometry, which gives the relationship between the lengths of sides of a right-angled triangle.

 

Pythagorean Theorem states that: “In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of perpendicular and base.”

 

i.e. h² = p² + b²

 

This Pythagorean relation is widely used in mathematics, physics, astrology, geology, engineering, etc.

 

Derived Relations

 

From the above Pythagorean relation, we can have the following derived relations:

 

Pythagorean Triple

 

A set of three positive integers a, b and c such that a² + b² = c² (Pythagorean relation) are called Pythagorean Triple. If {a, b, c} is a Pythagorean Triple, then so is {ka, kb, kc} for any positive integer k. Pythagorean triples that have the highest common factor 1 include the following: {3, 4, 5}, {5, 12, 13}, {8, 15, 17}, {7, 24, 25} and {20, 21, 29} etc.

 

Application of Pythagorean Theorem

 

Worked Out Examples

 

Example 1: The area of square A is 21cm² and the area of square C is 33cm², find the area of square B.

Solution: Here,

Area of square A = 21cm²

Area of square C = 33cm²

Area of square B =?

Using Pythagoras theorem,

Area of square C = Area of square A + Area of square B

i.e.     33cm² = 21cm² + Area of square B

or,     Area of square B = 33cm² – 21cm²

or,     Area of square B = 12cm²

 ∴ The area of square B is 12cm².

 

Example 2: Calculate the value of ‘x’ in the adjoining right-angled triangle.

Solution: Here,

From the adjoining figure,

Perpendicular (p) = 3cm

Base (b) = 4cm

Hypotenuse (h) = x = ?

We know that,

∴ x = 5cm

 

Example 3: The upper part of a tree is broken by the wind and the rest is 20m long. If the top of the tree lies 21m from the foot of the tree then find the length of the broken part of the tree.

 

Solution: Figure:

Height at which the tree has been broken (p) = 20m

The distance between the foot of the tree and the point where the broken part touches the ground (b) = 21m

Length of the broken part of the tree (h) =?

 

According to the Pythagoras theorem,

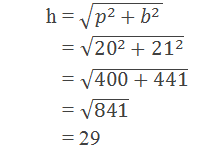
∴ The length of the broken part of the tree is 29m.