
A closed bounded geometrical figure with three or more sides is called a polygon. There are specific names of the polygon according to the number of sides in the polygon. They are as follows:

********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Interior and Exterior Angle of a Polygon
An angle that forms inside the polygon is called an interior angle. When a side of a polygon is produced, the angle that forms outside of the polygon is called an exterior angle.

The sum of interior angles of a polygon is given by the formula (n – 2) × 180° where n is the number of
sides of the polygon.
i.e. Sum of interior
angles of a polygon = (n – 2) × 180°
Therefore, by using this formula,
Sum of interior angles of a triangle = 180°
Sum of interior angles of a quadrilateral = 360°
Sum of interior angles of a pentagon = 540°
Sum of interior angles of a hexagon = 720°
Sum of interior angles of a heptagon = 900°
Sum of interior angles of an octagon = 1080°
Sum of interior angles of a nonagon = 1260°
Sum of interior angles of a decagon = 1440°
Sum of interior angles of a hendecagon = 1620°
Sum of interior angles of a dodecagon = 1800°
Regular Polygon
A polygon having all the sides equal and each interior angle also equal is called a regular polygon. The Interior and exterior angles of a regular polygon is given by the formula,
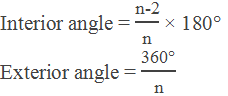
Construction of Regular Polygon
Example 1: Construct a regular pentagon of side 4 cm.
Solution: Here,
Length of side = 4 cm
No. of side (n) = 5
Interior angle = (n – 2)180°/n
= (5 – 2)180°/5
= 108°
Steps of construction:
Step 1: Draw a baseline XY and cut an arc of 4 cm on the line XY and
mark it AB.
Step 2: Draw 108° angle at points A and B using a protractor.
Step 3: Cut 4 cm arc AF and BG and mark as E and C.
Step 4: Make an angle of 108° at points E and C.
Step 5: Draw EH and CF and mark point D at the cross point.

Hence, ABCDE is a regular pentagon of side 4 cm.
Example 2: Construct a regular hexagon of side 3 cm.
Solution: Here,
Length of side = 3 cm
No. of side (n) = 6
Interior angle = (n – 2)180°/n
= (6 – 2)180°/6
= 120°
Steps of construction:
Step 1: Draw a baseline XY and cut an arc AB of 3 cm on XY.
Step 2: Make an angle 120° at each vertex and cut an arc of 3 cm in
each. Join the line segment.
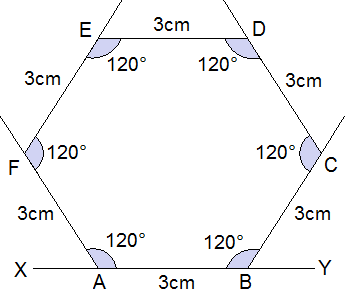
Hence, ABCDEF is a regular hexagon of side 3 cm.
Example 3: Construct a regular octagon of side 3.5 cm.
Solution: Here,
Length of side = 3.5 cm
No. of side (n) = 8
Interior angle = (n – 2)180°/n
= (8 – 2)180°/8
= 135°
Steps of construction:
Step 1: Draw a baseline XY and cut an arc AB of 3.5 cm on XY.
Step 2: Make an angle 135° at each vertex and cut an arc of 3.5 cm in
each. Join the line segment.
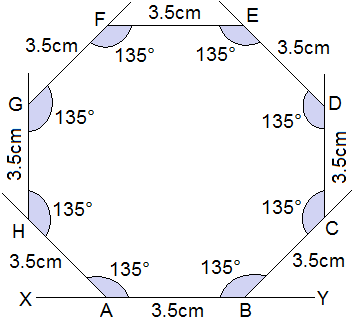
Hence, ABCDEFGH is a regular octagon of side 3.5 cm.
Worked Out Examples
Example 4: Find the value of x.

Solution: Here,
From the figure,
No. of sides (n) = 5
Sum of interior angles = (n – 2)180°
i.e. 3x + 4x + 2x + 2x + x = (5 – 2)180°
or, 12x = 540°
or, x = 540°/12
or, x = 45° Ans.
Example 5: Find the value of x.
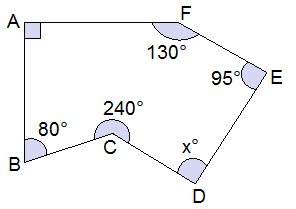
Solution: Here,
From the figure,
No. of sides (n) = 6
Sum of interior angles = (n – 2)180°
i.e. ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = (6 – 2)180°
or, 90° + 80° + 240° + x + 95° + 130° = 720°
or, x + 635° = 720°
or, x = 720° - 635°
or, x = 85° Ans.
Example 6: Find the number of sides of a regular polygon where each interior
angle is 120°.
Solution: Here,
Each interior angle = 120°
i.e. (n – 2)180°/n = 120°
or, (n – 2)180° = 120°n
or, 180°n - 360° = 120°n
or, 180°n - 120°n = 360°
or, 60°n = 360°
or, n = 360°/60°
or, n = 6
∴ Number of side (n) = 6 Ans.



0 comments: