
To check whether a number is exactly divisible by 2, or 3, or 5,
or 7, etc. we have to go through the actual division. But, it is time-consuming
and tedious performing actual division all the time. There are certain rules
for the test of divisibility of any number by 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, or
11 without performing the actual division. They are called divisibility rules.
Here are the divisibility rules of any number by 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, and 11.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Test of divisibility by 1
Every number is divisible by 1.
For example:
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 1 = 3
4 ÷ 1 = 4
5 ÷ 1 = 5 and so on.
Test of divisibility by 2
If the unit place digit of any number is 0 or even number, then
the number is divisible by 2. For example: In the number 1234, the unit place digit
4 which is an even number, so the number 1234 is divisible by 2.
Here,

Hence, 1234 ÷ 2 = 617 with no remainder.
Test of divisibility by 3
If the sum of the digits of any number is divisible by 3, then the
number is divisible by 3. For example: In a number 4251, the sum of its digits
= 4+2+5+1 = 12, and 12 is divisible by 3 with no remainder i.e. 12 ÷ 3 = 4. So,
the number 4251 is divisible by 3.
Here,
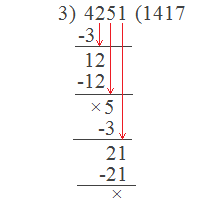
Hence, 4251 ÷ 3 = 1417 with no remainder.
Test of divisibility by 4
The number whose last two digits together is multiple of 4, then
the number is divisible by 4 with no remainder. For example: In a number 3464,
the number formed by the last two digits is 64, and it is a multiple of 4 i.e. 4 ×
16 = 64. So, the number 3464 is divisible by 4 with no remainder.
Here,
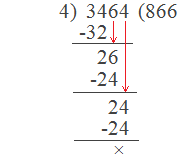
Hence, 3464 ÷ 4 = 866 with no remainder.
Test of divisibility by 5
The number is divisible by 5 if its unit place digit is 0 or 5.
For example: In a number 9565, the unit place digit is 5, so the number is
divisible by 5 with no remainder.
Here,

Hence, 9565 ÷ 5 = 1913 with no remainder.
Test of divisibility by 6
If the given number is an even number and the sum of its digits is a multiple of 3, then it is divisible by 6 with no remainder. For example: The
number 21234 is an even number and the sum of its digits = 2+1+2+3+4 = 12 which
is a multiple of 3. So, the number 21234 is divisible by 6 with no remainder.
Here,

Hence, 21234 ÷ 6 = 3539 with no remainder.
Test of divisibility by 7
If the given number is of 6 digits and all the digits are the
same, then the number is divisible by 7. For example: The numbers 222222,
333333, 444444, 555555, etc. are divisible by 7. Again, a number is divisible by
7 if the difference between twice of its unit place digit and the number formed by the rest is divisible by 7. For example: In a number 336, twice its unit digit =
2×6 = 12. And the number formed by the rest = 33. The difference = 33 – 12 = 21,
and 21 is divisible by 7. So, the number 336 is divisible by 7.
Here,

Hence, 336 ÷ 7 = 48 with no remainder.
Test of divisibility by 8
If the number formed by the last three digits of the given
number is divisible by 8, then the entire number is divisible by 8 with no
remainder. For example: In the number 43512, the number formed by the last three
digits is 512. And, 512 is divisible by 8 with no remainder i.e. 512 ÷ 8 = 64.
So, the number 43512 is exactly divisible by 8.
Here,

Hence, 43512 ÷ 8 = 5439 with no remainder.
Test of divisibility by 9
If the sum of digits of the given number is divisible by 9, the
number is divisible by 9 with no remainder. For example: In the number 13563,
the sum of digits = 1+3+5+6+3 = 18, and 18 is divisible by 9, hence the number
13563 is divisible by 9.
Here,

Hence, 13563 ÷ 9 = 1507 with no remainder.
Test of divisibility by 10
The number having 0 in its unit place is divisible by 10. For
example: The number 12340 has 0 in its unit place. So, this number is divisible
by 10.
Here,
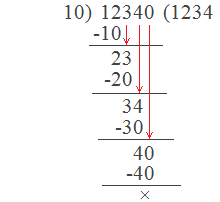
Hence, 12340 ÷ 10 = 1234 with no remainder.
Test of divisibility by 11
If the sum of digits at odd and even places are equal (or the difference is divisible by 11) then the number is divisible by 11. For example:
In the number 3245682,
Sum of digits at odd places = 3+4+6+2 = 15
Sum of digits at even places = 2+5+8 = 15
Here, both the sums are equal. Hence, as the rule, the number
3245682 is divisible by 11.
Here,

Hence, 3245682 ÷ 11 = 295062 with no remainder.
Divisibility Rules In Summary:
1.
Every number is divisible
by 1.
2.
If the unit place digit of
any number is 0 or even number, then the number is divisible by 2.
3.
If the sum of the digits
of any number is divisible by 3, then the number is divisible by 3.
4.
The number whose last two
digits together is multiple of 4, then the number is divisible by 4.
5.
The number is divisible by
5 if its unit place digit is 0 or 5.
6.
If the given number is
even number and the sum of its digits is multiple of 3, then the number is
divisible by 6.
7.
If the given number is of 6
digits and all the digits are the same, then the number is divisible by 7. Again, a number is divisible by 7 if the difference between twice of its unit place digit and the number formed by the rest is divisible by 7.
8.
If the number formed by
the last three digits of the given number is divisible by 8, then the number is
divisible by 8.
9.
If the sum of digits of
the given number is divisible by 9, then the number is divisible by 9.
10. The number having 0 in its
unit place is divisible by 10.
11. If the sum of digits at odd and even places are equal (or the difference is divisible by 11) then the number is divisible by 11.



0 comments: