Degree Measure (Sexagesimal System)

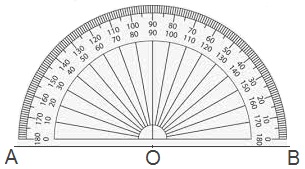
Look at the adjoining protractor in which a straight line AOB is divided into 180 small parts. Each part is a degree or 1°.

The most common unit of measurement of an angle is the degree. The system of measuring angles in degrees, minutes, and seconds is called Degree Measure or Sexagesimal System.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Degrees are divided by placing the vertex of the angle at the centre of a circle of some fixed radius. Then the circumference of the circle is divided into 360 equal parts, each part is called a degree.

 

In trigonometry, an angle is defined in different ways. In the adjoining figure, let O be a fixed point and OX a fixed-line. OP is a line which initially coincides OX and revolves about O. The amount of rotation of OP about O with respect to OX is called an angle between OX and OP and written as ∠POX. Initially, when OP coincides OX, there is no rotation and the angle formed is zero.

Hence, the amount of rotation of a revolving line about a fixed point with respect to the initial line is called an angle.

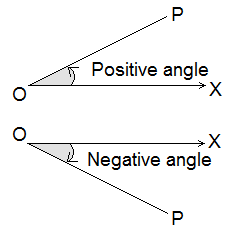
If OP rotates about O in an anticlockwise direction, the angle formed by this is positive and if OP rotates about O in a clockwise direction, the angle formed by this is negative.

If the line OP has made a complete rotation and again 60°, then the angle made by OP is 360° + 60° = 420°. Similarly, if OP has made two complete rotation and again 60° then the angle made by OP is 2×360° + 60° = 780° and so on.

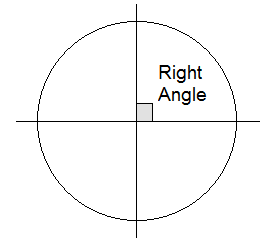
One-fourth of a complete rotation is called a right angle. In sexagesimal system, a right angle is divided into 90 equal parts and each part is called degree. Further, each degree is subdivided into 60 equal parts called minutes and each minute is subdivided into 60 equal parts called seconds.

We denote the degrees, minutes and seconds by the symbol (°), (ʹ) and (ʺ) respectively.

 

Thus, we have,

1 right angle = 90 degrees (90°)

1 degree = 60 minutes (60ʹ)

1 minute = 60 seconds (60ʺ)

 

So, 45° 50ʹ 55ʺ means 45 degrees, 50 minutes, and 55 seconds.

We have,

1 right angle = 90°

1° = 60ʹ

1ʹ = 60ʺ

 

 

Worked Out Examples

 

Example 1: Convert into sexagesimal seconds 45° 35ʹ 25ʺ.

 

Solution: Here,

45° 35ʹ 25ʺ = (45×60×60 + 35×60 + 25)ʺ

          = (162000 + 2100 + 25)ʺ

          = 164125ʺ Ans.

 

 

Example 2: Reduce 44° 30ʹ 45ʺ to the degrees.

 

Example 3: Express 60.1532° into degrees, minutes, and seconds.

 

Solution: Here,

60.1532° = 60° (0.1532×60)ʹ

          = 60° 9.192ʹ

          = 60° 9ʹ (0.192×60)ʺ

          = 60° 9ʹ 11.52ʺ Ans.