Cramer’s Rule

0 comments

Cramer’s Rule

 

Gabriel Cramer (1704-1752) was a great mathematician from Geneva. He showed his promise in mathematics from an early age. At the age of 18, he received his doctorate and at the age of 20, he was the Co-chair of mathematics at the University of Geneva.



English inventor Charles Babbage (1792-1871) knew a method for solving linear systems called Cramer’s Rule, in honor of the Swiss geometer Gabriel Cramer (1704-1752). Cramer’s rule was simple but involved numerous multiplications for large systems. Babbage designed a machine, called the “difference engine”, that consisted of toothed wheels on shafts for performing these multiplications. Despite the fact that only one-seventh of the functions ever worked, Babbage’s invention demonstrated how complex calculations could be handled mechanically. In 1944, scientists at IBM used the lessons of the difference engine to create the world’s first computer.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems

******************** 


 

Solving System of Linear Equations in Two Variables Using Determinants

 

Determinants can be used to solve a linear system of equations in two variables. In general, such a system appears as

 

a1x + b1y = c1 …………… (i)

a2x + b2y = c2 …………… (ii)

 

Let’s first solve this system by the elimination method. We can solve for x by eliminating y from the equations. Multiply the first equation by b2 and the second equation by –b1, then add the two equations:

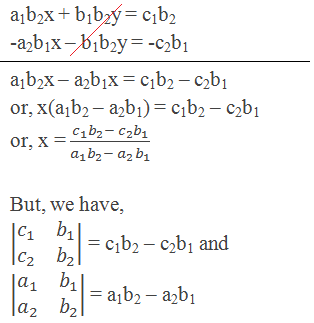
a1b2x + b1b2y = c1b2 -a2b1x – b1b2y = -c2b1 a1b2x – a2b1x = c1b2 – c2b1 or, x(a1b2 – a2b1) = c1b2 – c2b1 or, x = (c_1 b_2- c_2 b_1)/(a_1 b_2- a_2 b_1 ) But, we have, |■(c_1&b_1@c_2&b_2 )| = c1b2 – c2b1 and |■(a_1&b_1@a_2&b_2 )| = a1b2 – a2b1
 

So, we can express the value of x as the quotient of two determinants.

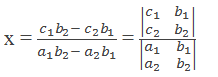
x = (c_1 b_2- c_2 b_1)/(a_1 b_2- a_2 b_1 ) = |■(c_1&b_1@c_2&b_2 )|/|■(a_1&b_1@a_2&b_2 )|


Similarly, multiply equation (i) by a2 and equation (ii) by –a1, then add the equations:

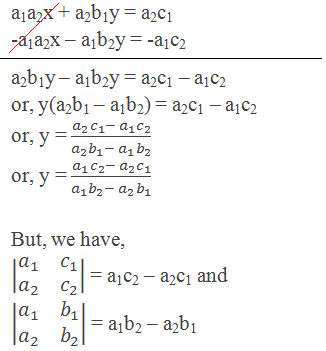
a1a2x + a2b1y = a2c1 -a1a2x – a1b2y = -a1c2 a2b1y – a1b2y = a2c1 – a1c2 or, y(a2b1 – a1b2) = a2c1 – a1c2 or, y = (a_2 c_1- a_1 c_2)/(a_2 b_1- a_1 b_2 ) or, y = (a_1 c_2- a_2 c_1)/(a_1 b_2- a_2 b_1 ) But, we have, |■(a_1&c_1@a_2&c_2 )| = a1c2 – a2c1 and |■(a_1&b_1@a_2&b_2 )| = a1b2 – a2b1

So, we can express the value of y as the quotient of two determinants.

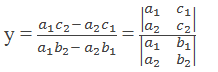
y = (a_1 c_2- a_2 c_1)/(a_1 b_2- a_2 b_1 ) = |■(a_1&c_1@a_2&c_2 )|/|■(a_1&b_1@a_2&b_2 )|

This method of using determinants to solve the linear system is called Cramer’s Rule.

 

 

Cramer’s Rule in Summary

 

If a1x + b1y = c1 and a2x + b2y = c2 are system of linear equations, then

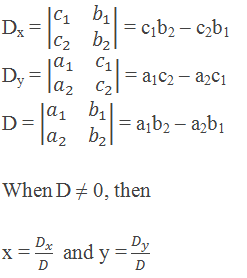
Dx = |■(c_1&b_1@c_2&b_2 )| = c1b2 – c2b1 Dy = |■(a_1&c_1@a_2&c_2 )| = a1c2 – a2c1 D = |■(a_1&b_1@a_2&b_2 )| = a1b2 – a2b1 When D ≠ 0, then x = D_x/D and y = D_y/D

This method of solving a system of linear equations is called Cramer’s Rule.

 

 

Worked Out Examples

 

Example 1: Solve simultaneous equations 5x – 4y = 2 and 6x – 5y = 1 by using Cramer’s rule.

 

Solution: Here,

5x – 4y = 2 …………. (i)

6x – 5y = 1 …………. (ii)

Coefficient of x Coefficient of y Constant term 5 -4 2 6 -5 1 Now, Dx = |■(2&-4@1&-5)| = 2×-5 - 1×-4 = -10 + 4 = -6 Dy = |■(5&2@6&1)| = 5×1 - 6×2 = 5 – 12 = -7 D = |■(5&-4@6&-5)| = 5×-5 - 6×-4 = -25 + 24 = -1 Using Cramer’s rule, x = D_x/D = (-6)/(-1) = 6 y = D_y/D = (-7)/(-1) = 7

Thus, x = 6 and y = 7   Ans.

 

 

Example 2: Use Cramer’s rule to solve the equations: x + 2y = 7 and 2x – y = 4.

 

Solution: Here,

x + 2y = 7 …………. (i)

2x – y = 4 …………. (ii)

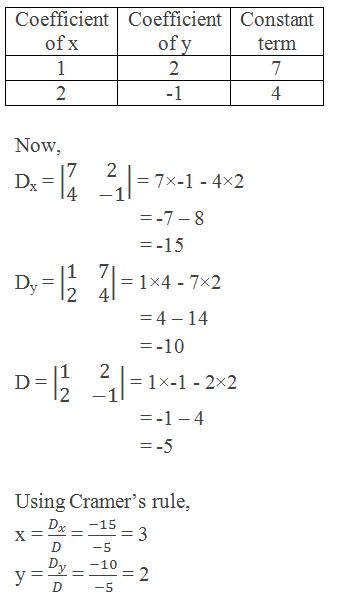
Coefficient of x Coefficient of y Constant term 1 2 7 2 -1 4 Now, Dx = |■(7&2@4&-1)| = 7×-1 - 4×2 = -7 – 8 = -15 Dy = |■(1&7@2&4)| = 1×4 - 7×2 = 4 – 14 = -10 D = |■(1&2@2&-1)| = 1×-1 - 2×2 = -1 – 4 = -5 Using Cramer’s rule, x = D_x/D = (-15)/(-5) = 3 y = D_y/D = (-10)/(-5) = 2

Thus, x = 3 and y = 2   Ans.

 

 

Example 3: Solve the following system of equations using Cramer’s rule:

5/x + 4/y = 58 and 7/x = 67 – 3/y

Solution: Here,

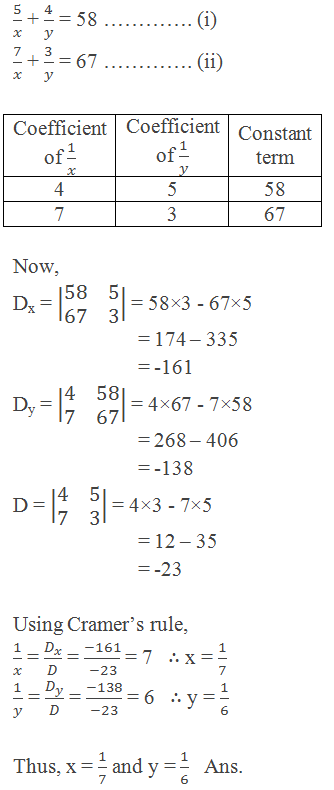
5/x + 4/y = 58 …………. (i) 7/x + 3/y = 67 …………. (ii) Coefficient of 1/x Coefficient of 1/y Constant term 4 5 58 7 3 67 Now, Dx = |■(58&5@67&3)| = 58×3 - 67×5 = 174 – 335 = -161 Dy = |■(4&58@7&67)| = 4×67 - 7×58 = 268 – 406 = -138 D = |■(4&5@7&3)| = 4×3 - 7×5 = 12 – 35 = -23 Using Cramer’s rule, 1/x = D_x/D = (-161)/(-23) = 7 ∴ x = 1/7 1/y = D_y/D = (-138)/(-23) = 6 ∴ y = 1/6 Thus, x = 1/7 and y = 1/6 Ans.



 

Labels:

0 comments:

Subscribe to: Post Comments (Atom)