
What is a Rational Number?
The definition of a rational number is “A number which can be
expressed in the form of p/q or fraction where p and q are integers
and q ≠ 0 is a Rational Number.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Examples of Rational Numbers
All the integers and decimal numberes can be expressed in the form of p/q or fraction of two integers. For example 0 = 0/1, 1 = 2/2, -2 = -4/2, 0.5 = ½, 1.25 = 5/4, 0.3333… = 1/3 etc. Therefore, 0, 1, -2, 0.5, 1.25, 0.3333… etc. are some examples of rational numbers
Rational numbers include all the integers on a number line along with the fractions between integers. Look at the number line given below.

The set of rational numbers is denoted by Q.
Q = {… -1, …, -¾, …, -½, …, -¼, …, 0, …, ¼, …, ½, …, ¾, …, 1, …}
Note:
- There
are infinitely many rational numbers between any two integers.
- There
are infinitely many rational numbers between any two rational numbers.
How to find rational numbers between two numbers?
We can find rational numbers between any two numbers by the
following two methods:
1. By
Mean Method
2. By
Fraction Method
By Mean Method
In this method, we find the middle value i.e. mean of the given two
numbers by dividing their sum by 2. Then again, we find the mean of the first
and the middle number by dividing their sum by 2. And, by continuing this procedure we can find any number of rational numbers between them.
Look at the following examples of finding rational numbers by mean
method.
Example 1: Find
6 rational numbers between 3 and 4.
Solution:
Here,
Six rational numbers between 3 and 4 by mean method are as
follows:
1st Number = (3+4)/2 = 7/2 = 3.5
2nd Number = (3+3.5)/2 = 6.5/2 = 3.25
3rd Number = (3+3.25)/2 = 6.25/2 = 3.125
4th Number = (3+3.125)/2 = 6.125/2 = 3.0625
5th Number = (3+3.0625)/2 = 6.0625/2 = 3.03125
6th Number = (3+3.03125)/2 = 6.03125/2 = 3.015625
∴
3.5, 3.25, 3.125, 3.0625, 3.03125 and 3.015625 are 6 rational numbers between 3
and 4.
Example 2: Find
five rational numbers between 3/4 and 4/5.
Solution:
Here,
Five rational numbers between 3/4 and 4/5 by the mean method are as follows:

∴ Five rational numbers between 3/4 and 4/5 are:

By Fraction Method
In this method, we convert the given numbers into the fractions of
equal denominators, then multiply the numerator and denominator by n+1 to both
the fractions to obtain n rational numbers between them.
Look at the following examples of finding rational numbers by
fraction method.
Example 3: Find five
rational numbers between 1 and 2.
Solution:
Here,
We need 5 rational numbers between 1 and 2. So, we have to multiply 6/6 to both the numbers to obtain 5 rational numbers between them.
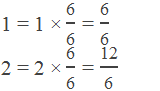
In between 6 and 12, there are 7, 8, 9, 10, and 11. Therefore, five rational numbers between 1 and 2 are:

Example 4: Find
3 rational numbers between 3/4 and 4/5.
Solution:
Here,
We can convert 3/4 and 4/5 into the rational number of common denominator 20 by multiplying first by 5 and second by 4. Then, we have to multiply 4/4 to both the rational numbers to obtain 3 more rational numbers between them as follows.

In between 60 and 64, there are 61, 62, and 63. Therefore, 3 rational numbers between ¾ and 4/5 are:

Properties of Rational Numbers
Following are the properties of Rational Numbers:
1. Rational Numbers are
closed under the operation of Addition, Subtraction, Multiplication and
Division.
i.e. if x, y ∈ Q, then x+y ∈ Q, x–y ∈ Q, x×y ∈ Q and x÷y ∈ Q.
2. Rational Numbers are Commutative.
i.e. if x, y ∈ Q, x+y = y+x and x×y =
y×x
3. Rational Numbers are Associative.
i.e. if x, y, z ∈ Q, (x+y)+z = x+(y+z)
4. Rational Numbers are Distributive.
i.e. if x, y, z ∈ Q, x×(y+z) = x×y + x×z
5. There is an Additive Identity
0, such that x+0=0+x=x.
6. There is a Multiplicative
Identity 1, such that x×1=1×x=x.
7. There exist an Additive Inverse
for every Rational Number.
i.e. if x ∈ Q there exist -x ∈ Q such that x+(-x)=(-x)+x=0 (Additive Identity)
8. There exist a Multiplicative
Inverse for every Rational Number.
i.e. if x ∈ Q there exist 1/x ∈ Q such that x×1/x=1/x×x=1 (Multiplicative Identity)
Rational Numbers and Decimals
When we convert a rational number into the decimal form, the
number so obtained may be terminating or non terminating decimal. In the case of
non-terminating decimal, a digit or a block of digits after the decimal point
gets repeated after certain intervals. Such decimals are termed non-terminating recurring decimals. For example:
1/3 = 0.3333333…
5/11 = 0.454545…
But others decimals that get terminated are called terminating
decimals. For example:
1/4 = 0.25
2/5 = 0.4
Questions and Answers on Rational Numbers
Is 0 a rational number?
Answer:
Yes, 0 is a rational
number because it can be expressed in the form of p/q like 0/1, 0/2, 0/3, etc.
Is 1 a rational number?
Answer:
Yes, 1 is a rational
number because it can be expressed in the form of p/q like 1/1, 2/2, 3/3, etc.
Is 2 a rational number?
Answer:
Yes, 2 is a rational
number because it can be expressed in the form of p/q like 2/1, 4/2, 6/3, etc.
Is 3 a rational number?
Answer:
Yes, 3 is a rational
number because it can be expressed in the form of p/q like 3/1, 6/2, 9/3, etc.
Is 4 a rational number?
Answer:
Yes, 4 is a rational
number because it can be expressed in the form of p/q like 4/1, 8/2, 12/3, etc.
Is 5 a rational number?
Answer:
Yes, 5 is a rational
number because it can be expressed in the form of p/q like 5/1, 10/2, 15/3, etc.
Is pi(π) a rational number?
Answer:
No, pi(π) is not a
rational number. 22/7 is not the exact value of pi. It is just an approximation. The value of pi(π) is non-terminating and non-recurring decimal 3.14159265358979323846… which is an
irrational number.
If you have any questions or problems regarding the Rational Numbers, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: