Integers

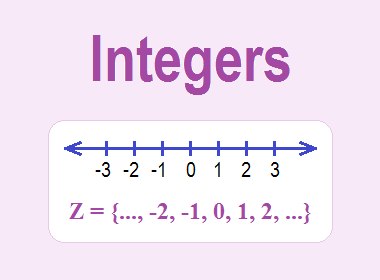
What is Integer?

 

The definition of integer is “Any counting number whether it is negative(-), positive(+) or zero(0) is an integer.”

 

The set of integers is an infinite set from both the sides and it is denoted by Z.

Z = {…… -5, -4, - 3, -2, -1, 0, 1, 2, 3, 4, 5 ......}

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Integer Number line

 

The numbers represented by a numbered line with negatives and zero (0) are all integers. So, it is called an Integer Number Line, or negative and positive number line, or negative to positive number line, or simply an integer line.

 

What are positive integers?

 

The integers toward the right side from zero (0) are positive integers.

Positive integers (Z⁺): +1, +2, +3, +4, +5, ……

 

 

What are negative integers?

 

The integers toward the left side from zero (0) are negative integers.

Negative integers (Z^–):  ……, -5, -4, -3, -2, -1

 

 

Is zero (0) an integer?

 

Yes, zero (0) is an integer. It is neither positive(+) nor negative(-). It is a constant integer.

 

 

Properties of integers

 

Following are the properties of integers:

 

1.    Integers are closed under the operation of Addition, Subtraction and Multiplication.

i.e. if x, y ∈ Z, then x+y ∈ Z, x–y ∈ Z and x×y ∈ Z.

2.    Integers are Commutative.

i.e. if x, y ∈ Z, x+y = y+x  and x×y = y×x

3.    Integers are Associative.

i.e. if x, y, z ∈ Z, (x+y)+z = x+(y+z)

4.    Integers are Distributive.

i.e. if x, y, z ∈ Z, x×(y+z) = x×y + x×z

5.    There is an Additive Identity 0, such that x+0=0+x=x.

6.    There is a Multiplicative Identity 1, such that x×1=1×x=x.

7.    There exist an Additive Inverse for every integer.

i.e. if x ∈ Z there exist -x ∈ Z such that x+(-x)=(-x)+x=0 (additive identity)

8.    There does not exist Multiplicative Inverse in integers.

 

Addition of Integers

 

The integers with the same signs are always added and the same sign will be in the result also.

 

For example:

(+2) + (+3) = +5

(-3) + (-5) = - 8

 

And, the integers with different signs are always subtracted and the sign of greater integer will be in the result.

 

For example:

(+8) + (-3) = +5

(-7) + (+3) = - 4

 

How to use a number line to find the sum of two integers?

 

Rules:

 

1.    Draw a number line.

2.    To draw the arrows, move toward the right if the integer is positive, and move toward the left if the integer is negative.

3.    Sketch the arrow of the first integer starting from 0.

4.    Sketch the arrow of the second integer from the ending point of first integer.

5.    The final point will give the sum of the integers.

 

For example:

(+2) + (+3)

Hence, (+2) + (+3) = +5

 

(-3) + (-5)

Hence, (-3) + (-5) = - 8

 

(+8) + (-3)

Hence, (+8) + (-3) = +5

 

(-7) + (+3)

Hence, (-7) + (+3) = - 4

 

 

Subtraction of Integers

 

In subtraction of integers, we change the sign of the integer that has to be subtracted and do same as the addition of integers.

 

For example:

(-5) – (+3) = (-5) + (-3) = -8

(+2) – (-5) = (+2) + (+5) = +7 etc.

 

 

Multiplication of Integers

 

The product of two integers of the same sign are always positive (+).

 

For example:

(+2) × (+4) = (+8)

(-3) × (-2) = (+6)

 

But, the product of two integers of opposite signs is negative (-).

 

For example:

(+2) × (-4) = (-8)

(-3) × (+2) = (-6)

 

How to use a number line to find the product of two integers?

 

Rules:

 

1.    Draw a number line.

2.    Sketch arrow of the first integer starting from 0 and the number of times of the second integer.

3.    Move to the right if both the integers are of the same sign.

4.    Move to the left if both the integers are of different signs.

5.    The final point will be the product of the integers.

 

For example:

(+2) × (+4)

Hence, (+2) × (+4) = (+8)

         

(-3) × (-2)

Hence, (-3) × (-2) = (+6)

 

(+2) × (-4)

Hence, (+2) × (-4) = (-8)

 

(-3) × (+2)

Hence, (-3) × (+2) = (-6)

 

Division of Integers

 

In the division of integers, if both the integers in dividend and divisor are of the same signs, the quotient is positive.

 

For example:

(+8) ÷ (+2) =  (+4)

(-6) ÷ (-3) = (+2)

 

But, if both the integers in dividend and divisor are of opposite signs, the quotient is negative.

 

For example:

(-8) ÷ (+2) = (-4)

(+6) ÷ (-3) = (-2)

 

How to use a number line to find the divide of integers?

 

Rules:

 

1.    Draw a number line.

2.    Sketch arrow of the integer in divisor starting from 0 and the number of times until it reaches the integer of the dividend.

3.    Move to the right if both the integers are of the same sign.

4.    Move to the left if both the integers are of different signs.

5.    The number of arrows will be the quotient.

 

For example:

(-8) ÷ (+2)

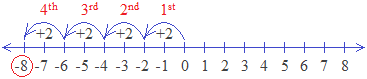
Hence, (-8) ÷ (+2) = (-4)

 

(+6) ÷ (-3)

Hence, (+6) ÷ (-3) = (-2)

 

Questions and Answers

 

What are the differences between rational numbers and integers?

Answer: 

Rational numbers are all whole numbers, fractions, and decimal numbers. But the integers are only the whole numbers. So, all integers are rational numbers, but all rational numbers are not integers. Every integer is a rational number with denominator 1.

 

 

Are all natural numbers integers?

Answer: 

Yes, all the natural numbers are integers. They are positive integers.

 

 

Are all whole numbers integers?

Answer: 

Yes, all whole numbers are integers. They are positive integers except 0.

 

 

Are all integers real numbers?

Answer: 

Yes, all integers are real numbers.

 

 

Which is the smallest integer?

Answer: 

The smallest integer is - ∞.

 

 

Which is the largest negative integer?

Answer: 

The largest negative integer is -1.

 

 

Which is the smallest negative integer?

Answer: 

The smallest negative integer is – ∞.

 

Which is the smallest positive integer?

Answer: 

The smallest positive integer is +1.

 

 

What are even integers?

Answer: 

Even numbers among the integers are the even integers.

 

 

What are odd integers?

Answer: 

Odd numbers among the integers are the odd integers.

 

 

What are consecutive integers?

Answer: 

The integers that come continuously one after another without the break on a number line are called consecutive integers. For example, -2, -1, 0, 1, 2, 3 are consecutive integers.

 

 

Write any three consecutive integers.

Answer: 

Any three consecutive integers are: (+3, +4, +5) or (+20, +21, +22) or (-1, 0, +1) etc.

 

 

Write any two consecutive integers.

Answer: 

Any two consecutive integers are: (+2, +3) or (+10, +11) or (-6, -5) etc.

 

 

What are consecutive even integers?

Answer: 

The even integers that come continuously one after another are called consecutive even integers. For example, 2, 4, 6, 8, 10, 12, etc.

 

Write any three consecutive even integers.

Answer: 

Any three consecutive even integers are: (+4, +6, +8) or (+12, +14, +16) or (+28, +30, +32) etc.

 

 

What are consecutive odd integers?

Answer: 

The odd integers that come continuously one after another are called consecutive odd integers. For example, 1, 3, 5, 7, 9, 11, etc.

 

 

Write any three consecutive odd integers.

Answer: 

Any three consecutive odd integers are: (+3, +5, +7) or (+11, +13, +15) or (+25, +27, +29) etc.

 

 

What are consecutive positive integers?

Answer: 

The positive integers that come continuously one after another are called consecutive positive integers. For example, +1, +2, +3, +4, +5, etc.

 

What are the perfect square integers?

Answer: 

The integers that are perfect squares numbers are called the perfect square integers. They are: +1, +4, +9, +16, +25, +36 etc.

 

 

What are non-integer numbers?

Answer: 

Except for integers, all rational numbers are non-integer numbers.

 

 

What are non-negative integers?

Answer: 

All positive integers are non-negative integers.

 

 

What are non-zero integers?

Answer: 

Except 0, all integers are non-zero integers.

 

 

What are odd integers from 1 to 100?

Answer: 

Odd integers from 1 to 100 are: +1, +3, +5, +7, +9, …., +99

 

 

What is Greatest Integer Function? Give examples.

Answer: 

The Greatest Integer Function of any real number x is an integer x if it a whole number, or an integer just left to x on the number line if it a fraction or decimal. It is denoted by ⌊x⌋.

 

For example,

⌊7⌋ = 7

⌊0.9⌋ = 0

⌊2.35⌋ = 2

⌊-5.36⌋ = -6

 

The Greatest Integer Function is also known as the Floor Function.

 

 

What are Gaussian Integers?

Answer: 

In Complex Number System, a complex number a + bi is said to be the Gaussian Integer if both a and b are integers. The set of Gaussian Integers is denoted by Z[i].

 

 

If you have any questions or problems regarding the Integers, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…