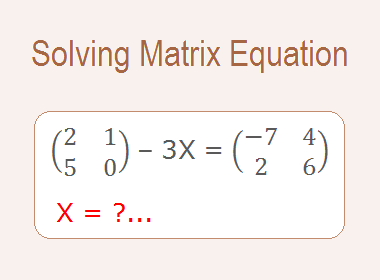
Solving Matrix Equations

Solving Matrix Equations

While solving matrix equation A + X = B, where A and B are two given matrices of the same order and X is an unknown matrix, we proceed in a manner similar to the numbers.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

Install Quick Math Solver

********************

Install 10 Math Problems

********************

Here, A + X = B

Adding the matrix (-A) to both sides of the matrix equation, we get -

(-A) + A + X = (-A) + B

or, (-A + A) + X = B – A

or, 0 + X = B – A

or, X = B – A,

which is the required solution of matrix equation A + X = B.

Worked Out Examples

Example 1: If A = (■(3&-4@0&1)) and B = (■(0&2@3&-1)), find the matrix X if 2A + X = 5B. Solution: Here, A = (■(3&-4@0&1)) and B = (■(0&2@3&-1)) We have, 2A + X = 5B or, X = 5B – 2A or, X = 5(■(0&2@3&-1)) - 2(■(3&-4@0&1)) or, X = (■(0&10@15&-5)) - (■(6&-8@0&2)) or, X = (■(0-6&10+8@15-0&-5-2)) or, X = (■(-6&18@15&-7))

Example 2: Solve the matrix equation (■(2&1@5&0)) – 3X = (■(-7&4@2&6)). Solution: Here, (■(2&1@5&0)) – 3X = (■(-7&4@2&6)) or, – 3X = (■(-7&4@2&6)) - (■(2&1@5&0)) or, -3X = (■(-7-2&4-1@2-5&6-0)) or, -3X = (■(-9&3@-3&6)) or, X = 1/(-3) (■(-9&3@-3&6)) or, X = (■((-9)/(-3)&3/(-3)@(-3)/(-3)&6/(-3))) or, X = (■(3&-1@1&-2))

Example 3: If A = (■(9&1@5&3)) and B = (■(1&5@7&-11)), find matrix X such that 3A + 5B – 2X = O, where O is null matrix. Solution: Here, A = (■(9&1@5&3)), B = (■(1&5@7&-11)) and O = (■(0&0@0&0)) We have, 3A + 5B – 2X = O i.e. 3(■(9&1@5&3)) + 5(■(1&5@7&-11)) – 2X = (■(0&0@0&0)) or, (■(27&3@15&9)) + (■(5&25@35&-55)) – 2X = (■(0&0@0&0)) or, (■(27+5&3+25@15+35&9-55)) – 2X = (■(0&0@0&0)) or, (■(32&28@50&-46)) – 2X = (■(0&0@0&0)) or, – 2X = (■(0&0@0&0)) - (■(32&28@50&-46)) or, – 2X = (■(0-32&0-28@0-50&0+46)) or, – 2X = (■(-32&-28@-50&46)) or, X = 1/(-2) (■(-32&-28@-50&46)) or, X = (■((-32)/(-2)&(-28)/(-2)@(-50)/(-2)&46/(-2))) or, X = (■(16&14@25&-23))

Example 4: Find the matrices A and B, if A + B = (■(7&0@2&5)) and A – B = (■(3&0@0&3)). Solution: Here, A + B = (■(7&0@2&5)) .............. (i) A – B = (■(3&0@0&3)) .............. (ii) Adding matrix equations (i) and (ii), we get A + B + A – B = (■(7&0@2&5)) + (■(3&0@0&3)) or, 2A = (■(7+3&0+0@2+0&5+3)) or, A = 1/2 (■(10&0@2&8)) or, A = (■(5&0@1&4)) Now, putting A = (■(5&0@1&4)) in matrix equation (i), we get (■(5&0@1&4)) + B = (■(7&0@2&5)) or, B = (■(7&0@2&5)) - (■(5&0@1&4)) or, B = (■(7-5&0-0@2-1&5-4)) or, B = (■(2&0@1&1)) ∴ A = (■(5&0@1&4)) and B = (■(2&0@1&1)).

Example 5: If 2(■(3&4@5&x)) + (■(1&y@0&1)) = (■(7&0@10&5)), find x and y. Solution: Here, 2(■(3&4@5&x)) + (■(1&y@0&1)) = (■(7&0@10&5)) or, (■(6&8@10&2x)) + (■(1&y@0&1)) = (■(7&0@10&5)) or, (■(7&8+y@10&2x+1)) = (■(7&0@10&5)) Equating the corresponding elements, we have 2x + 1 = 5 or, 2x = 5 – 1 or, 2x = 4 or, x = 2 And, 8 + y = 0 or, y = 0 – 8 or, y = - 8 ∴ x = 2 and y = - 8.

Example 6: Find x and y if (■(x+y@x-y)) = (■(10@2)). Solution: Here, (■(x+y@x-y)) = (■(10@2)) Equating the corresponding elements, we have x + y = 10 ……………… (i) x – y = 2 ……………….. (ii) Adding equations (i) and (ii), we get x + y + x – y = 10 + 2 or, 2x = 12 or, x = 12/2 or, x = 6 Now, putting x = 6 in equation (i), we get 6 + y = 10 or, y = 10 – 6 or, y = 4 ∴ x = 6 and y = 4.

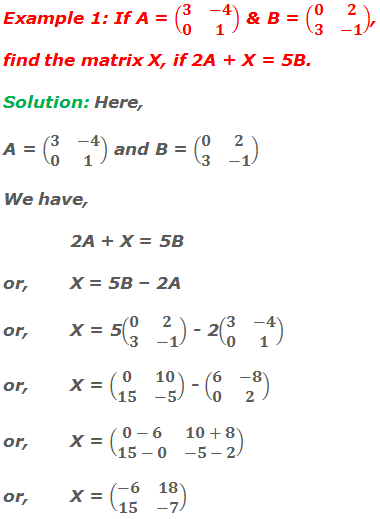
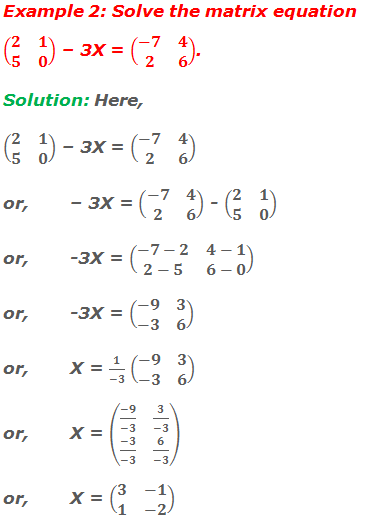
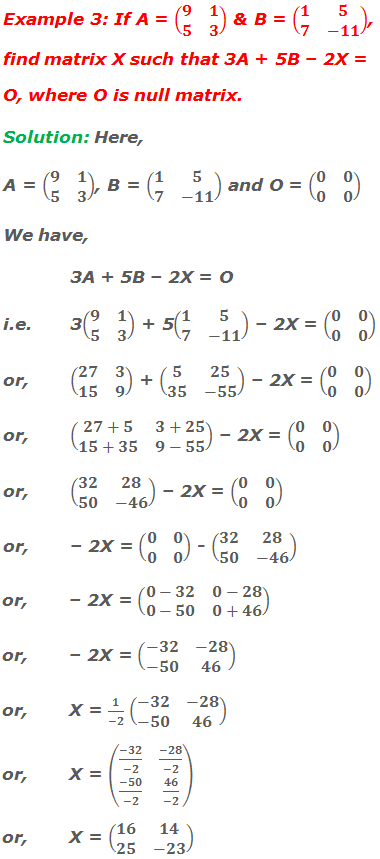
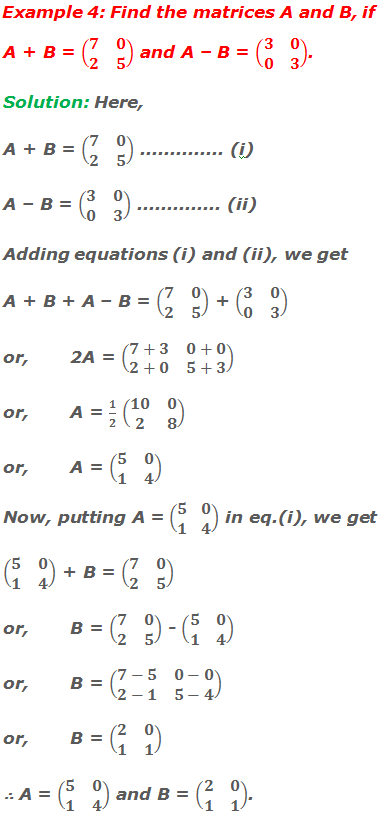
Do you have any questions regarding the solution of matrix equations?

You can ask your questions or problems here, in the comment section below.

0 comments:

Subscribe to: Post Comments (Atom)