Inverse of a Matrix

Inverse of a Matrix

If A is a non-singular square matrix i.e. |A| ≠ 0, and there exists another square matrix B such that AB = BA = I where I is an identity matrix of order same as that of A or B, then the matrix B is said to be the inverse of matrix A and vice-versa. The inverse of A is denoted by A^-1. ∴ B = A^-1.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Note: For the existence of the inverse of a matrix, the following requirements are necessary:

i)    The matrix must be a square matrix. This requirement is essential because, let A be a matrix of order 2×3 and B be another matrix of order 3×2, then AB and BA both exist but have different orders, namely 2×2 and 3×3 and hence cannot be equal.

ii)   The equation AB = BA = I (Identity Matrix) must be satisfied. For example, if

But, AB = BA ≠ I. So, they are not inverse matrix to each other.

iii)  The matrix must be non-singular. i.e |A| ≠ 0.

Method of Finding an Inverse Matrix

Some Properties of Inverses

a.   The inverse of the product of two non-singular matrices is equal to the product of their inverses taken in reverse order. i.e. If A and B are two non-singular matrices of same order then (AB)^-1 = B^-1A^-1.

b.   The transpose and inverse of a non-singular matrix is commutative. i.e. (A^-1)^t = (A^t)^-1.

Worked Out Examples

Do you have any questions regarding the inverse of a matrix?

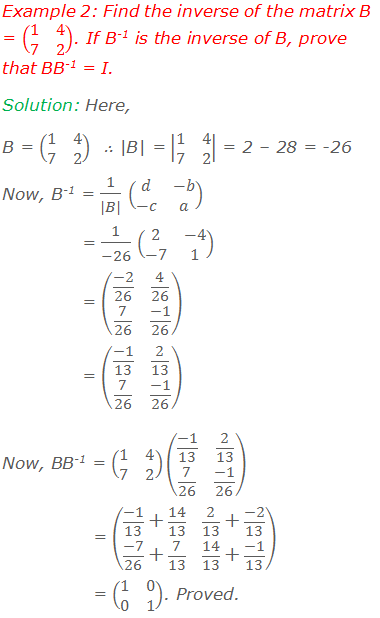
You can ask your questions or problems here, in the comment section below.