
Determinant of a Matrix
Determinants
originally appeared in the study of the linear equations. We shall, however,
associate the notion of the determinant with matrices. For this purpose, we
have to consider the square matrices of order 1, 2, 3 etc.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
If A is a
square matrix, its determinant is denoted by |A| or det.(A). And, the value of
determinant is calculated differently for different ordered square matrices. Here
is mentioned about the calculation of determinants of square matrices of order
1, 2 and 3.
Determinant of a 1×1 Matrix
Let A =
(a11) be a square matrix of order 1×1. Then, its determinant |A| is given
simply by the value of its single element a11.
i.e. |A|
= |a11| = a11
For
example: Let, A = (2), then
Determinant
of A = |A| = |2| = 2
Determinant of a 2×2 Matrix

Determinant of a 3×3 Matrix

Here is
an easy pattern to find the minors of any element of a 3×3 matrix:

Note: Determinant of 3×3 matrix
A can also be calculated by taking the products of the elements of any row (or
column) and the corresponding cofactors. i.e.
|A| = a11A11
+ a12A12 + a13A13
Or,
|A| = a21A21
+ a22A22 + a23A23
Or,
|A| = a31A31
+ a32A32 + a33A33
Or,
|A| = a11A11
+ a21A21 + a31A31
Or,
|A| = a12A12
+ a22A22 + a32A32
Or,
|A| = a13A13
+ a23A23 + a33A33
All will
give the same value for the determinant of A.
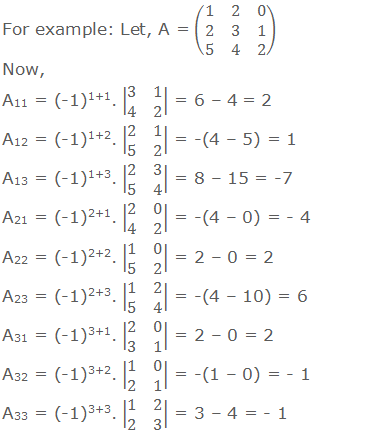
Now,
|A| = a11A11
+ a12A12 + a13A13 = 1×2 + 2×1 + 0×-7
= 4
|A| = a21A21
+ a22A22 + a23A23 = 2×-4 + 3×2 +
1×6 = 4
|A| = a31A31
+ a32A32 + a33A33 = 5×2 + 4×-1 +
2×-1 = 4
|A| = a11A11
+ a21A21 + a31A31 = 1×2 + 2×-4 +
5×2 = 4
|A| = a12A12
+ a22A22 + a32A32 = 2×1 + 3×2 +
4×-1 = 4
|A| = a13A13
+ a23A23 + a33A33 = 0×-7 + 1×6 +
2×-1 = 4
Here, we
got |A| = 4 in every calculations, so we can use any one of the above methods.
Generally, we use the first method to calculate the determinant of a 3×3 matrix
A. i.e.
|A| = a11A11
+ a12A12 + a13A13
Mechanical Rule (Rule of Sarrus)
A mechanical rule for finding the value of a third order determinant is as indicated below:-

From the algebraic sum of the products of the elements of the diagonals pointing
downwards, subtract the algebraic sum of the products of the elements of the
diagonals pointing upwards.
This rule
of expansion of a third-order determinant is known as The Rule of Sarrus.
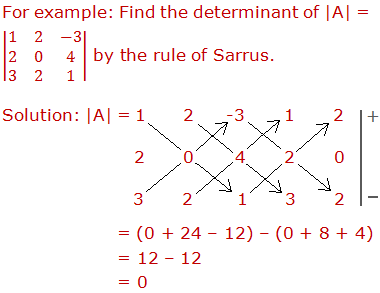
Note: This rule does
not work for the determinants of the order greater than 3.
Properties of 3×3 Determinant
We have
seen how to evaluate a 3×3 determinant. There are some properties of 3×3
determinant. Look at them and their verification.
Prop. 1: The value of the determinant is unaltered by interchanging
its rows and columns.
Verification:
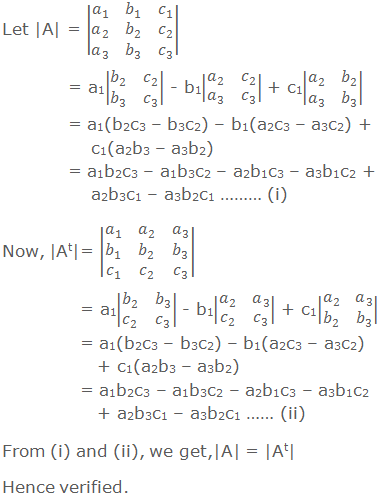
Prop. 2: Interchanging any two adjacent rows (or columns)
changes the sign of the determinant.
Verification:

Prop. 3: If any two rows (or columns) of a determinant are identical,
then the value of the determinant is zero.
Verification:

Prop. 4: If all the elements of any row (or column) are
multiplied by a constant k, then the value of the determinant is multiplied by k.
Verification:

Prop. 5: If each element of any row (or column) of a determinant
is expressed as the sum of two terms, then the determinant can be expressed as
the sum of determinants.
Verification:
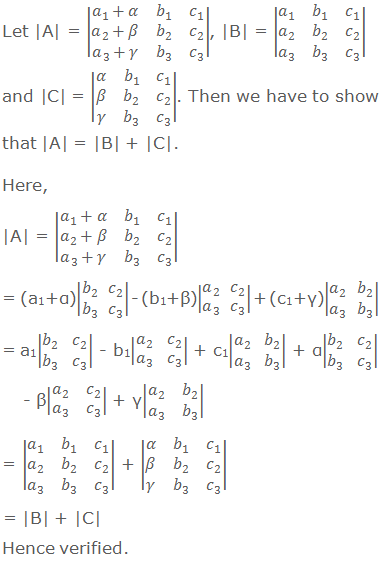
Prop. 6: If to the elements of any row (or column) a multiple of
any other row (or column) is added, the value of the determinant remains
unaltered.
Verification:

Worked Out Examples
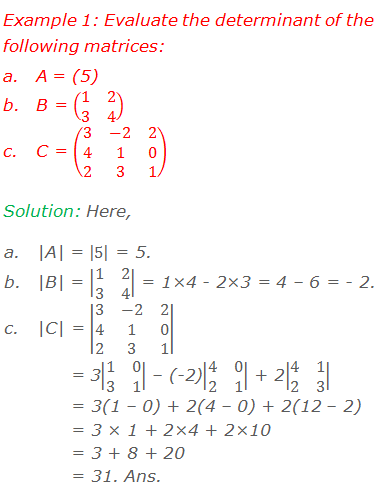
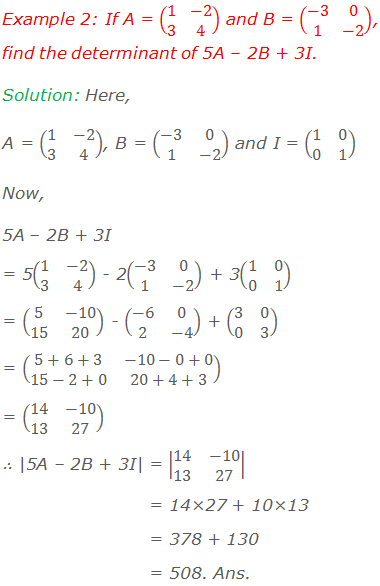
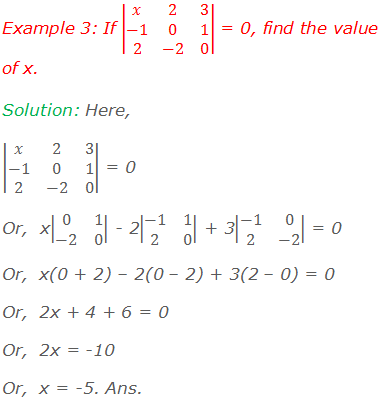
![Example 4 Example 4: Without expanding, show that |■(30&2&5@18&4&3@6&8&1)| = 0. Solution: Here, |■(30&2&5@18&4&3@6&8&1)| = |■(6×5&2&5@6×3&4&3@6×1&8&1)| = 6 |■(5&2&5@3&4&3@1&8&1)| [Taking 6 common from Column 1] = 6 × 0 [∵ Col. 1 = Col. 3] = 0](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgWiIm8H7WbRuIfflDKIHvjISPPGDRfviQFrCRGthTIgAbQmag040PP1HOD85zDCUFPstknie9xekqLx5aGiv95L_iAdUFpR2M0lXVxAz09UfnJjpg7sZV5P5yyqHj7xQMxnKVzVwVmS1Xf/s16000/example+4.png)

![Example 6 Example 6: Without expanding the determinant show that |■(b-c&b+c&b@c-a&c+a&c@a-b&a+b&a)| = 0. Solution: Here, LHS = |■(b-c&b+c&b@c-a&c+a&c@a-b&a+b&a)| = |■(2b&b+c&b@2c&c+a&c@2a&a+b&a)| [Adding column 1 and 2 i.e. applying C1 + C2] = 2 |■(b&b+c&b@c&c+a&c@a&a+b&a)| [Taking 2 common from C1] = 2 × 0 [∵ C1 = C3] = 0 = RHS.](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjL5eshLtV4KK1U5coHr1tLkR_UZBJnn1CJmaEElSnXe2uRw6__iIUQvqPJe6F8MSYFw56GdGH9IC37ywZYl6Tliwm43ub064QDBZn0Y6-MNKt4tXaFmuW103fiiTm5Y4Th6dk3ZfHr-EKH/s16000/example+6.png)
![Example 7 Example 7: Show that |■(1&x&x^2@1&y&y^2@1&z&z^2 )| = (x – y)(y – z)(z – x). Solution: Here, LHS = |■(1&x&x^2@1&y&y^2@1&z&z^2 )| = |■(1&x&x^2@0&y-x&y^2-x^2@0&z-x&z^2-x^2 )| [Applying R2 – R1, R3 – R1] = |■(1&x&x^2@0×(y-x)&y-x&(y+x)(y-x)@0×(z-x)&z-x&(z+x)(z-x))| = (y – x)(z – x) |■(1&x&x^2@0&1&y+x@0&1&z+x)| [Taking (y – x) common from R2 and (z – x) from R3] = (y – x)(z – x) |■(1&y+x@1&z+x)| = (y – x)(z – x)(z + x – y – x) = (y – x)(z – x)(z – y) = (x – y)(y – z)(z – x) = RHS. Proved.](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhtZ4PfElnPOm1z2MhmeXzmptxJ6O-YUoT8Mk8l57efnLGj38i7zlGkP0mxSPqHXA3_UvQWXm3LkGc0v9gT4_FQYyT7uCpjcbi9QBAJzSwwnNSAKyKlpwt08M2eyyb09GPuwsahUuqfRfU7/s16000/example+7.png)
Do you have any questions regarding the determinant of a matrix?
You can ask your questions or problems here, in the comment section below.



0 comments: