Adjoint of a Matrix

0 comments

Adjoint of a Matrix

Adjoint of a Matrix


Let A be a square matrix, and Aij be the cofactors of the elements aij of the matrix A, then adjoint or adjugate of A denoted by adj A is the matrix obtained by transposing the matrix of cofactors of A.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************


Let A = (■(a_11&a_12&a_13@a_21&a_22&a_23@a_31&a_32&a_33 )) be a 3×3 matrix, and Aij be the cofactor of element aij, then adjoint or adjugate of A is defined by, adj A = transpose of (■(A_11&A_12&A_13@A_21&A_22&A_23@A_31&A_32&A_33 )) = (■(A_11&A_21&A_31@A_12&A_22&A_31@A_13&A_23&A_33 ))


For example:


i. Let A = (■(2&4@1&3)), then we have, a11 = 2, a12 = 4, a21 = 1 and a22 = 3. And, their cofactors are: A11 = 3, A12 = -1, A21 = -4 and A22 = 2. Then, by definition, adj A = transpose of (■(A_11&A_12@A_21&A_22 )) = (■(A_11&A_21@A_12&A_22 )) = (■(3&-4@-1&2))


ii. Let A = (■(1&2&-2@-1&3&0@0&-2&1)), then we have, a11 = 1, a12 = 2, a13 = -2, a21 = -1, a22 = 3, a23 = 0, a31 = 0, a32 = -2 and a33 = 1. And, their cofactors are: A11 = cofactor of a11 = |■(3&0@-2&1)| = 3-0=0 A12 = cofactor of a12 = - |■(-1&0@0&1)| = -(-1-0)=1 A13 = cofactor of a13 = |■(-1&3@0&-2)| = 2-0=2 A21 = cofactor of a21 = - |■(2&-2@-2&1)| = -(2-4)=2 A22 = cofactor of a22 = |■(1&-2@0&1)| = 1-0=1 A23 = cofactor of a23 = - |■(1&2@0&-2)| = -(-2-0)=2 A31 = cofactor of a31 = |■(2&-2@3&0)| = 0+6=6 A32 = cofactor of a32 = - |■(1&-2@-1&0)| = -(0-2)=2 A33 = cofactor of a33 = |■(1&2@-1&3)| = 3+2=5 Thus by definition, adj A = transpose of (■(A_11&A_12&A_13@A_21&A_22&A_23@A_31&A_32&A_33 )) = (■(A_11&A_21&A_31@A_12&A_22&A_31@A_13&A_23&A_33 )) = (■(3&2&6@1&1&2@2&2&5))

Inverse of Matrices by Adjoint Method


Let us take an example of a 3×3 matrix A = (■(2&2&-2@-2&3&0@0&-2&1)). Here, |A| = |■(2&4&-4@-1&3&0@0&-2&1)| = 2|■(3&0@-2&1)| - (-2) |■(2&-2@-2&1)| + 0|■(2&-2@3&0)| = 2(3 – 0) + 2(2 – 4) + 0(0 + 3) = 6 – 4 + 0 = 2 So, A is a non-singular matrix i.e. |A| ≠ 0. Now, let’s find the cofactors of A. A11 = cofactor of a11 = |■(3&0@-2&1)| = 3 + 0 = 3 A12 = cofactor of a12 = - |■(-2&0@0&1)| = -(-2 – 0) = 2 A13 = cofactor of a13 = |■(-2&3@0&-2)| = 4 – 0 = 4 A21 = cofactor of a21 = - |■(2&-2@-2&1)| = -(2 – 4) = 2 A22 = cofactor of a22 = |■(2&-2@0&1)| = 2 – 0 = 2 A23 = cofactor of a23 = - |■(2&2@0&-2)| = -(-4 – 0) = 4 A31 = cofactor of a31 = |■(2&-2@3&0)| = 0 + 6 = 6 A32 = cofactor of a32 = - |■(2&-2@-2&0)| = -(0 – 4) = 4 A33 = cofactor of a33 = |■(2&2@-2&3)| = 6 + 4 = 10 Now, by definition adj A = transpose of (■(A_11&A_12&A_13@A_21&A_22&A_23@A_31&A_32&A_33 )) = (■(A_11&A_21&A_31@A_12&A_22&A_31@A_13&A_23&A_33 )) = (■(3&2&6@2&2&4@4&4&10)) Now, let us calculate A.(adj A) and (adj A).A, A.(adj A) = (■(2&2&-2@-2&3&0@0&-2&1))(■(3&2&6@2&2&4@4&4&10)) = (■(6+4-8&4+4-8&12+8-20@-6+6+0&-4+6+0&-12+12+0@0-4+4&0-4+4&0-8+10)) = (■(2&0&0@0&2&0@0&0&2)) = 2.(■(1&0&0@0&1&0@0&0&1)) = |A|.I (adj A).A = (■(3&2&6@2&2&4@4&4&10))(■(2&2&-2@-2&3&0@0&-2&1)) = (■(6-4-0&6+6-12&-6+0+6@4-4+0&4+6-8&-4+0+4@8-8+0&8+12-20&-8+0+10)) = (■(2&0&0@0&2&0@0&0&2)) = 2.(■(1&0&0@0&1&0@0&0&1)) = |A|.I Thus, we see that, A.(adj A) = (adj A).A = |A|.I Or, (A.(adj A))/(|A|) = ((adj A).A)/(|A|) = I Or, A.(adj A)/(|A|) = (adj A)/(|A|).A = I (Identity Matrix) Thus, (adj A)/(|A|) behaves as the inverse of A. ∴ if A is a non-singular matrix, i.e. |A| ≠ 0, then the inverse of matrix A is given by the formula, A-1 = (adj A)/(|A|)

Worked Out Examples


Example 1: Find the inverse of (■(3&2@-1&6)). Solution: Let A = (■(3&2@-1&6)), then |A| = 18 + 2 = 20 adj A = transpose of (■(A_11&A_12@A_21&A_22 )) = (■(A_11&A_21@A_12&A_22 )) = (■(6&-2@1&3)) ∴ A-1 = (adj A)/(|A|) = 1/20 (■(6&-2@1&3)) = (■(6/20&(-2)/20@1/20&3/20)) = (■(3/10&(-1)/10@1/20&3/20))


Example 2: Find the inverse of (■(1&2&-1@2&0&1@0&3&-1)). Solution: Let A = (■(1&2&-1@2&0&1@0&3&-1)) |A| = |■(1&2&-1@2&0&1@0&3&-1)| = 1|■(0&1@3&-1)| - 2|■(2&-1@3&-1)| + 0|■(2&-1@0&1)| = 1(0 – 3) – 2(–2 + 3) + 0(2 – 0) = –3 – 2 + 0 = –5 Now, A11 = cofactor of a11 = |■(0&1@3&-1)| = 0 – 3 = -3 A12 = cofactor of a12 = - |■(2&1@0&-1)| = -(-2 – 0) = 2 A13 = cofactor of a13 = |■(2&0@0&3)| = 6 – 0 = 6 A21 = cofactor of a21 = - |■(2&-1@3&-1)| = -(-2 + 3) = -1 A22 = cofactor of a22 = |■(1&-1@0&-1)| = -1 – 0 = -1 A23 = cofactor of a23 = - |■(1&2@0&3)| = -(3 – 0) = -3 A31 = cofactor of a31 = |■(2&-1@0&1)| = 2 – 0 = 2 A32 = cofactor of a32 = - |■(1&-1@2&1)| = -(1 + 2) = -3 A33 = cofactor of a33 = |■(1&2@2&0)| = 0 – 4 = -4 ∴ adj A = transpose of (■(A_11&A_12&A_13@A_21&A_22&A_23@A_31&A_32&A_33 )) = (■(A_11&A_21&A_31@A_12&A_22&A_31@A_13&A_23&A_33 )) = (■(-3&-1&2@2&-1&-3@6&-3&-4)) ∴ A-1 = (adj A)/(|A|) = 1/(-5) (■(-3&-1&2@2&-1&-3@6&-3&-4)) = (■(3/5&1/5&(-2)/5@(-2)/5&1/5&3/5@(-6)/5&3/5&4/5))

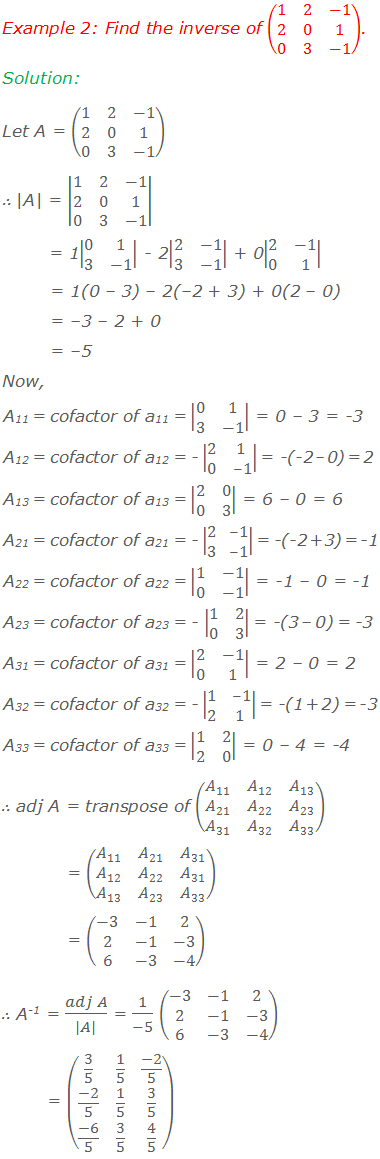
Do you have any questions regarding the adjoint of a matrix?


You can ask your questions or problems here, in the comment section below.

Labels:

0 comments:

Subscribe to: Post Comments (Atom)