
Trigonometric Ratios of Allied Angles
If θ is any angle, then the angle of the form 90°+θ, 90°–θ,
180°+θ, 180°–θ, 270°+θ etc. are called allied
angles. We can find the trigonometric
ratios of allied angles in terms of the trigonometric ratios of angle θ.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
This can be done easily by applying the concept of reflection
and rotation of a point in co-ordinate plane as follows:
Trigonometric Ratios of Angle θ
Consider an angle θ placed in the standard position. Draw circle with centre at O and radius r. Let the circle intersect the terminal line at some point P(x, y) as shown in the figure. Draw perpendicular PM from P to the x-axis. Then MP = y, OM = x and OP = r.

sinθ = y/r cosθ
= x/r tanθ = y/x
cosecθ = r/y secθ = r/x cotθ = x/y
Trigonometric Ratios of (90° – θ)
Reflect the point P(x, y) in the line y = x. Then the image of P(x, y) under this reflection is P’(y, x). Join OP’. Then ∠XOP’ = 90° - θ.

Now,
sin(90° – θ) = x/r = cosθ
cosec(90° – θ) = r/x = secθ
cos(90° – θ) = y/r = sinθ
sec(90° – θ) = r/y = cosecθ
tan(90° – θ) = x/y = cotθ
cot(90° – θ) = y/x = tanθ
Trigonometric Ratios of (90° + θ)
Rotate the point P(x, y) about origin through 90° in anticlockwise (positive) direction. Then the image of P(x, y) under this rotation is P’(–y, x). Join OP’. Then ∠XOP’ = 90° + θ.

Now,
sin(90° + θ) = x/r = cosθ
cosec(90° + θ) = r/x = secθ
cos(90° + θ) = –y/r = – sinθ
sec(90° + θ) = r/–y = – cosecθ
tan(90° + θ) = x/–y = – cotθ
cot(90° + θ) = –y/x = – tanθ
Trigonometric Ratios of (180° – θ)
Reflect the point P(x, y) in the line Y–axis. Then the image of P(x, y) under this reflection is P’(–x, y). Join OP’. Then ∠XOP’ = 180° – θ.

Now,
sin(180° – θ) = y/r = sinθ
cosec(180° – θ) = r/y = cosecθ
cos(180° – θ) = –x/r = – cosθ
sec(180° – θ) = r/–x = – secθ
tan(180° – θ) = y/–x = – tanθ
cot(180° – θ) = –x/y = – cotθ
Trigonometric Ratios of (180° + θ)
Rotate the point P(x, y) about origin through 180° in anticlockwise (positive) direction. Then the image of P(x, y) under this rotation is P’(–x, –y). Join OP’. Then ∠XOP’ = 180° + θ.

Now,
sin(180° + θ) = –y/r = – sinθ
cosec(180° + θ) = r/–y = – cosecθ
cos(180° + θ) = –x/r = – cosθ
sec(180° + θ) = r/–x = – secθ
tan(180° + θ) = –y/–x = tanθ
cot(180° + θ) = –x/–y = cotθ
Trigonometric Ratios of (270° – θ)
Reflect the point P(x, y) in the line y = – x. Then the image of P(x, y) under this reflection is P’(– y, – x). Join OP’. Then ∠XOP’ = 270° – θ.

Now,
sin(270° – θ) = –x/r = – cosθ
cosec(270° – θ) = r/–x = – secθ
cos(270° – θ) = –y/r = – sinθ
sec(270° – θ) = r/–y = – cosecθ
tan(270° – θ) = –x/–y = cotθ
cot(270° – θ) = –y/–x = tanθ
Trigonometric Ratios of (270° + θ)
Rotate the point P(x, y) about origin through 270° in anticlockwise (positive) direction. Then the image of P(x, y) under this rotation is P’(y, – x). Join OP’. Then ∠XOP’ = 270° + θ.

Now,
sin(270° + θ) = –x/r = – cosθ
cosec(270° + θ) = r/–x = – secθ
cos(270° + θ) = y/r = sinθ
sec(270° + θ) = r/y = cosecθ
tan(270° + θ) = –x/y = – cotθ
cot(270° + θ) = y/–x = – tanθ
Trigonometric Ratios of (360° – θ) or (– θ)
Reflect the point P(x, y) in the line X–axis. Then the image of P(x, y) under this reflection is P’(x, – y). Join OP’. Then ∠XOP’ = 360° – θ. Also, ∠XOP’ in clockwise direction = – θ.

Now,
sin(360° – θ) = sin(– θ) = –y/r = – sinθ
cosec(360° – θ) = cosec(– θ) = r/–y = – cosecθ
cos(360° – θ) = cos(– θ) = x/r = cosθ
sec(360° – θ) = sec(– θ) = r/x = secθ
tan(360° – θ) = tan(– θ) = –y/x = – tanθ
cot(360° – θ) = cot(– θ) = x/–y = – cotθ
Signs of the Trigonometric Ratios
We have seen that the trigonometric ratios has different signs in different quadrants. The following table shows the sign of all the trigonometrc ratios of angles in different quadrants.
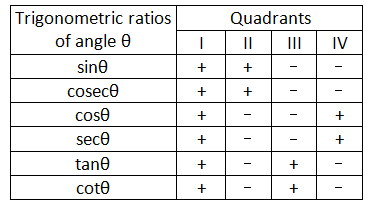
The sign of the trigonometric ratios of an angle of any
magnitude can be remembered from the diagram as shown.
Trigonometric Ratios of Any Angle
Any angle can be expressed in the form (n × 90° ± θ) where n is
an integer. And, we can change the trigonometric ratios of the angle (n × 90° ±
θ) into the trigonometric ratio of angle θ.
Here are the ideas to express trigonometric ratios of a higher
angle to smaller angle:
1. Express the given
angle in the form (n × 90° ± θ) where n is an integer.
2. If n is even number,
there will be no change in the trigonometric ratios. i.e.
sin(n × 90° ± θ) ⇒ sinθ,
cos(n × 90° ± θ) ⇒ cosθ
etc.
3. If n is odd number,
then the trigonometric ratios change as follows:
sin(n × 90° ± θ) ⇒ cosθ
cosec(n × 90° ± θ) ⇒ secθ
cos(n × 90° ± θ) ⇒ sinθ
sec(n × 90° ± θ) ⇒ cosecθ
tan(n × 90° ± θ) ⇒ cotθ
cot(n × 90° ± θ) ⇒ tanθ
4. The sign of the trigonometric ratio of the angle (n × 90° ± θ) is determined by taking into consideration that in which quadrant the angle (n × 90° ± θ) lies.
For example: Find the ratio of sin570°.
Solution:
Here, 570° = 6 × 90° + 30°. Therefore 570° lies in 7th
quadrant i.e. in 3rd quadrant where the ratio of sin will be
negative. And, n = 6 is an even number, so no change in trigonometric ratio.
∴ sin570° = sin(6 × 90° +
30°)
= – sin30°
= – ½
Trigonometric Ratios of Higher Standard Angles
Trigonometric Ratios of 120°
sin120° = sin(1 × 90° + 30°) = cos30° = √3/2
cosec120° = cosec(1 × 90° + 30°) = sec30° = 2/√3
cos120° = cos(1 × 90° + 30°) = – sin30° = – ½
sec120° = sec(1 × 90° + 30°) = – cosec30° = – 2
tan120° = tan(1 × 90° + 30°) = – cot30° = – √3
cot120° = cot(1 × 90° + 30°) = – tan30° = – 1/√3
Trigonometric Ratios of 135°
sin135° = sin(1 × 90° + 45°) = cos45° = 1/√2
cosec135° = cosec(1 × 90° + 45°) = sec45° = √2
cos135° = cos(1 × 90° + 45°) = – sin45° = – 1/√2
sec135° = sec(1 × 90° + 45°) = – cosec45° = – √2
tan135° = tan(1 × 90° + 45°) = – cot45° = – 1
cot135° = cot(1 × 90° + 45°) = – tan45° = – 1
Trigonometric Ratios of 150°
sin150° = sin(1 × 90° + 60°) = cos60° = 1/2
cosec150° = cosec(1 × 90° + 60°) = sec60° = 2
cos150° = cos(1 × 90° + 60°) = – sin60° = – √3/2
sec150° = sec(1 × 90° + 60°) = – cosec60° = – 2/√3
tan150° = tan(1 × 90° + 60°) = – cot60° = – 1/√3
cot150° = cot(1 × 90° + 60°) = – tan60° = – √3
Trigonometric Ratios of 180°
sin180° = sin(1 × 90° + 90°) = cos90° = 0
cosec180° = cosec(1 × 90° + 90°) = sec90° = ∞
cos180° = cos(1 × 90° + 90°) = – sin90° = – 1
sec180° = sec(1 × 90° + 90°) = – cosec90° = – 1
tan180° = tan(1 × 90° + 90°) = – cot90° = 0
cot180° = cot(1 × 90° + 90°) = – tan90° = ∞
Table of Trigonometric Ratios of Standard Angles

Worked Out Examples
Example 1: Find the value of tan855°.
Solution: Here,
Tan855° = tan(9 ×
90° + 45°)
= –
cot45°
= –
1 Ans.
Example 2: Prove that: tan25° + sin35° + sec40° = cot65° + cos55° + cosec50°
Solution: Here,
LHS = tan25° + sin35° +
sec40°
= tan(90° – 65°)
+ sin(90° – 55°) + sec(90° – 50°)
= cot65° + cos55°
+ cosec50°
= RHS. Proved.
Example 3: Find the value of A if sin3A = cosA.
Solution: Here,
sin3A = cosA
or, sin3A = sin(90° –
A)
∴ 3A = 90° – A
or, 3A + A = 90°
or, 4A = 90°
or, A = 90°/4
or, A = 22.5° Ans.
Example 4: Prove that: cos (π/8) + cos (3π/8) + cos(5π/8) + cos(7π/8) = 0
Solution: Here,
LHS = cos (π/8) + cos (3π/8) + cos(5π/8) + cos(7π/8)
= cos(π – 7π/8) +
cos(π – 5π/8) + cos(5π/8) + cos(7π/8)
= – cos(7π/8) –
cos(5π/8) + cos(5π/8) + cos(7π/8)
= 0
= RHS. Proved.
Example 5: If A, B, C are the angles of a triangle, show that: sin(A+B) = sinC
Solution: Here,
A + B + C = 180°
[Sum of angles of a triangle is 180°]
or, A + B = 180° – C
or, sin(A + B) =
sin(180° – C) [Putting sin to both side]
or, sin(A + B) = sinC
Proved.
If you have any question or problems regarding the Trigonometric Ratios of Allied Angles,
you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: