Solution of Right Angled Triangle

Solution of Right Angled Triangle

 

A triangle has three sides and three angles. Angles and sides together are said to be the six parts of a triangle.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

In a right-angled triangle, one angle is 90°, so there are 5 parts unknown.

 

Under a given condition, the finding of the unknown parts of a right angled triangle is known as the solution of a right-angled triangle.

 

Let ABC be a right-angled triangle, right-angled at B. We denote its angles ∠CAB, ∠ABC, and ∠BCA by A, B, and C respectively.

Here, B = 90°.

 

The sides opposite to angles A, B, and C are denoted by a, b and c respectively. So, BC = a, CA = b and AB = c.

 

Then,

By Pythagoras relation h² = p² + b², we have

b² = a² + c²

 

Again, by the sum of two acute angles,        

A + C = 90°

 

If we know one side and any one of the remaining four parts, we can find the other parts of the right-angled triangle. This process of calculating the unknown parts is known as the solution of a right-angled triangle.

 

Methods of Solving a Right Angled Triangle

 

- When two sides of a right-angled triangle are given

(i)        When a and c, are given.

Then, b² = a² + c².

∴  b = √(a² + c²)

Again, sinA = a/b and so A is found.

At last, C = 90° - A.

(ii)     When, a and b are given.

Then, c² = b² – a².

∴  c = √(b² – a²)

Again, sinA = a/b and it gives A.

At last, C = 90° - A.

 

- When one side and one acute angle are given

(i)        When A and b are given.

Then, C = 90° - A

sinA = a/b

∴  a = b sinA

cosA = c/b

∴  c = b cosA

(ii)     When, A and a are given.

Then, C = 90° - A

sinA = a/b

∴  b = a/sinA = a cosecA

cosA = c/b

∴  c = b cosA

 

 

Worked Out Examples

 

Example 1: Find the unknown angles and the sides of the following right angled triangles:

 

Solution:

(i)        Figure: Right angled triangle ABC

In DABC, ∠B = 90°, ∠C = 45° and BC = √2

∠A = 90° – ∠C = 90° – 45° = 45°

 

Now,

tan45° = AB/BC

or,   1 = AB/√2

or,   AB = √2

 

Again,

cos45° = BC/AC

or,   1/√2 = √2/AC

or,   AC = 2

 

∴  ∠A = 45°, AB = √2 and AC = 2  Ans.

 

(ii)     Figure: Triangle ABC

In triangle ABC,  AB = √3, BC = 1 and AC = 2

Now,

AB² + BC² = (√3)² + (1)²

                   = 3 + 1

                   = 4

                   = (2)²

                   = AC²

Since, AB² + BC² = AC²

∴  ∠B = 90°

 

Now,

sinC = AB/AC

or,   sinC = √3/2

or,   sinC = sin60°

∴     C = 60°

 

And, ∠A = 90° – C = 90° – 60° = 30°

 

∴  ∠B = 90°, ∠C = 60°, and ∠A = 30° Ans.

 

Example 2: Solve the right angled triangle ABC in which ∠C = 90°, ∠B = 30° and a = 4√3 cms.

Solution: Here,   

In DABC, ∠C = 90°, ∠B = 30° and a = BC = 4√3 cms.

∠A = 90° – C = 90° – 30° = 60°

 

Now,

cos30° = BC/AB

or,     √3/2 = 4√3/AB

or,     AB√3 = 8√3

or,     AB = 8√3/√3 = 8 cms.

 

Again,

sin30° = AC/AB

or,     1/2 = AC/8

or,     2AC = 8

or,     AC = 8/2 = 4 cms.

 

∴  c = AB = 8cms, b = AC = 4cms, and ∠A = 60°  Ans.

 

 

Example 3: In a right angled triangle ABC, if ∠B = 90°, a = 2√3 and b = 4, find the remaining angles and the sides.

Solution: Here,

In triangle ABC,

∠B = 90°

a = BC = 2√3

b = AC = 4

         

Now,

cosC = BC/AC = 2√3/4 = √3/2 = cos30°

∴ C = 30°

 

And,

∠A = 90° – C = 90° – 30° = 60°

 

Again,

sin30° = AB/AC

or,     1/2 = AB/4

or,     2AB = 4

or,     AB = 4/2 = 2

 

∴  ∠A = 60°, ∠C = 30°, and c = AB = 2  Ans.

 

 

Example 4: Solve the triangle ABC if ∠A = 90°, b = 16 and c = 16.

Solution: Here,

In triangle ABC,

∠A = 90°

b = AC = 16

c = AB = 16

 

Since ∠A = 90°, so a is the hypotenuse.

 

∴   a² = b² + c²

          = (16)² + (16)²

          = 2 × (16)²

or,  a = 16√2

 

Now,

tanB = AC/AB = b/c = 16/16 = 1 = tan45°

∴  B = 45°

 

And,

∠C = 90° – B = 90° – 45° = 45°

 

∴  ∠B = 45°, ∠C = 45° and a = BC = 16√2 Ans.

 

Example 5: Solve the triangle ABC if a = 5√3, b = 5 and c = 10.

Solution: Here,

In triangle ABC,

a = BC = 5√3

b = AC = 5

c = AB = 10

 

Now,

AC² + BC² = (5)² + (5√3)²

                   = 25 + 75

                   = 100 = (10)² = AB²

Since,  AC² + BC² = AB²

∴  ∠C = 90°

 

Now,

cosA = AC/AB = 5/10 = ½ = cos60°

∴  A = 60°

 

And,

∠B = 90° – A = 90° – 60° = 30°

 

∴  ∠C = 90°, ∠B = 30°, and ∠A = 60° Ans.

 

 

Example 6: Solve a triangle ABC if ∠B = 60°, ∠A = 30° and a = 20.

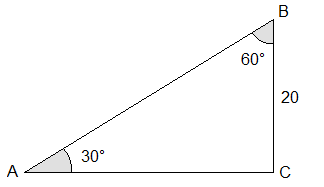
Solution: Here,

In triangle ABC,

∠B = 60°

∠A = 30°

a = BC = 20

 

Now,

∠C = 180° – (∠A + ∠B)

      = 180° – (30° + 60°)

      = 180° – 90°

      = 90°

 

And,

sin30° = BC/AB

or,     1/2 = 20/AB

or,     AB = 40

 

Again,

cos30° = AC/AB

or,     √3/2 = AC/40

or,     2AC = 40√3

or,     AC = 40√3/2 = 20√3

 

∴  ∠C = 90°, c = AB = 40 and b = AC = 20√3 Ans.

 

Example 7: In a right angled triangle the sides containing the right angle are 4√3cm and 12cm. Find the hypotenuse and acute angles.

Solution: Here,

In triangle ABC,

∠B = 90°

c = AB = 4√3cm.

a = BC = 12cm.

 

Now,

tanC = AB/BC = 4√3/12 = 1/√3 = tan30°

∴  C = 30°

 

And,

∠A = 90° – C = 90° – 30° = 60°

 

Again,

sinC = AB/AC

or,     sin30° = 4√3/AC

or,     ½ = 4√3/AC

or,     AC = 8√3 cm.

 

∴  ∠A = 60°, ∠C = 30°, and hypotenuse = AC = 8√3cm. Ans.

 

Example 8: Solve the triangle ABC if a = 3, b = 4 and c = 5 [Take cos54° = 3/5]

Solution: Here,

In triangle ABC,

a = BC = 3

b = AC = 4

c = AB = 5

 

Now,

a² + b² = 3² + 4² = 9 + 16 = 25 = 5² = c²

i.e.  a² + b² = c²

∴  ∠C = 90°

 

Again,

cosB = a/c = 3/5 = cos54°

∴  B = 54°

 

And,   ∠A = 90° – B

       = 90° – 54°

       = 36°

 

∴  ∠A = 36°, ∠B = 54° and ∠C = 90° Ans.

 

 

If you have any questions or problems regarding the Solution of Right Angled Triangle, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…