
Length of Circular Arc
There is a relationship between the arc of a circle, the circular measure of the central angle
and the radius of the circle. Which is,
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
"The
radian measure of an angle at the centre of a circle is equal to the ratio of
the subtending arc to the radius of the circle."
i.e. central angle = (length of arc / radius of
circle)c
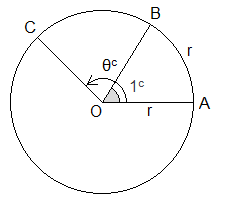
Let O be the centre of the circle and OA = r be the
radius of the circle cut an arc AB = r and join AB. Then by definition ∠AOB
= 1 radian. Also let arc ABC = s and ∠AOC
= θc.
Since, the angles at the centre of a circle are
proportional to their corresponding arc on which they stand,
i.e. ∠AOC/∠AOB
= arc ABC/arc AB
or, θc/1c
= s/r
or, θ = s/r
And, by transposing we have, s = θ × r and r = s/θ
Note:- To apply the above formulae, θ must
be in radian.
Look at the following workout examples:
Example 1: Find in degree the angle subtended at the centre of a
circle of radius 5.6cm by an arc of length 22cm.
Solution: Here,
Radius of the circle (r) = 5.6cm
Length of arc (s) = 22cm
Angle at the centre (θ) = ?
By
using formula,
θ = s/r
= 22cm/5.6cm
= 3.9286 radian
= (3.9286 × 180/π)° [∵ 1c
= (180/π)°]
= (3.9286 × 180/3.14)° [∵ π
= 3.14]
= 225°
Example 2: The given figure is a part of the circle with centre O
and the arc AB. If OA = 14cm and ∠AOB = (3π/4)c, calculate the length of the arc AB. Also, find the
perimeter of the figure OAB.
Solution: Here,
The radius of the given sector (r) =
14cm
The angle at centre (θ) = (3π/4)c
Length of arc AB (s) = ?
We
have,
s = θ × r
= (3π/4)
× 14
= 3/4 × 22/7 × 14 [Putting π =
22/7]
= 33cm
Perimeter
of sector OAB = OA + OB + arc AB
= 14cm + 14cm + 33cm
= 61cm
Example 3: A horse is tied to a stake by rope of length 50 m. If the
horse moves around the boundary of the circle always keeping the rope tight,
find how far will it have gone when the rope has traced out an angle of 63° at
the centre.
Solution: Here,
Radius of the circle (r) = 50m
Central angle (θ) = 63° = (63 × π/180)c
= (7π/20)c
Length of an arc AB (s) = ?
By
using formula,
s = θ × r
= (7π/20)
× 50
= 7/20 × 22/7 × 50 [Putting π =
22/7]
= 55m
Hence,
the horse has gone about 55 meters.
Example 4: If the radius of the earth is 6400 km and the distance of
the moon from the earth is 60 times the radius of the earth, find the radius of
the moon which subtends at the earth the angle of 16’.
Solution: Let, O be the position of the earth
and OA = OB is the distance between the earth and the moon. As the distance
between moon and earth is very large, diameter AB of moon can be considered as
the arc of a circle with centre O and radius OA.
Hence,
Radius of circle (r) = 60
× 6400 km
Central angle (θ) = 16’ =
(16/60)° = (4/15 × π/180)c
= (π/675)c
Diameter of moon (AB = s) =?
By
using formula,
s = θ × r
= π/675
× 60 × 6400
= 22/7 × 1/675 × 60 × 6400 [Putting
π =
22/7]
= 1787.937 km
Hence
the diameter of the moon, AB = 1787.937 km.
And,
its radius = 1787.937/2 = 893.968 km.
Example 5: What is the ratio of the radii of two circles at the
centre of which two arcs of the same length subtend angles of 80° and 120°?
Solution: Let, r1 and r2
be the radii of the first and the second circles respectively. If s be the
length of arc of both circles,
Then,
s/r1 = θ1
= circular measure of 80°
= 80 × π/180
= 4π/9
………………… (i)
And,
s/r2 = θ2
= circular measure of 120°
= 120 × π/180
= 2π/3
………………… (ii)
Now,
dividing equation (ii) by (i),
(s/r2)/(s/r1) =
(2π/3)/(4π/9)
or, r1/r2 = 3/2
i.e. r1:r2 = 3:2
Hence,
the required ratio is 3:2.
You can comment your questions or problems regarding the circular arc, radius and central angle of a circle here.







0 comments: