Tangents of a Circle

Tangents of a Circle

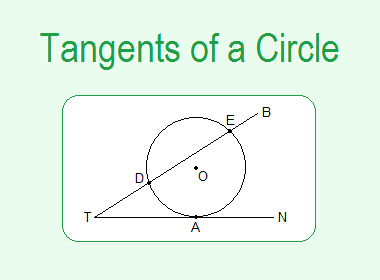
A line which is drawn from an external point of a circle and meets the circle at one and only point on the circumference is called a tangent of a circle. 

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

The point A where tangent touches the circle is called the point of contact.

In the figure, TAN is a line which meets the circle at a point A. So TAN is a tangent and the point A is point of contact.

In the same figure, a line TB cuts the circle at two points D and E. So the line TB is called a secant.

 

Properties of tangent:

1.    A tangent to a circle is perpendicular to the radius of the circle drawn at point of contact.

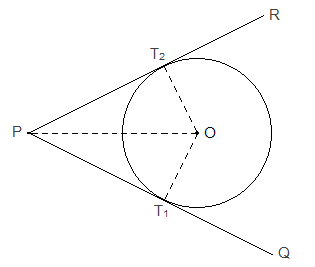
2.     The length of two tangents drawn from an external point to a circle are always equal.

Angles in alternate segments

In the figure given below, PQ is a tangent to a circle at the point of contact T. A chord TA is drawn from the point of contact T. Here the chord TA divides the circle into two segments, TBA and TCA. These two segments are called alternate segments.

Here, for ∠ATP, the alternate segment is TBA.

And, for ∠ATQ, the alternate segment is TCA.

So, ∠ATP and ∠TBA are said to be the alternate segment angles and, ∠ATQ and ∠TCA are also said to be the alternate segment angles.

The alternate segment angles are always equal.

Circle theorems on tangents:

1.    A tangent to a circle is perpendicular to the radius of the circle drawn at point of contact.

2.    The length of two tangents drawn from an external point to a circle are always equal.

3.    The alternate segment angles are always equal.

 

Proofs:

1.   A tangent to a circle is perpendicular to the radius of the circle drawn at point of contact.

Given: O is centre of the circle. PQ is a tangent to circle at point of contact T.

To Prove: OT ⊥ PQ

Construction: Any point R is taken on PQ and OR is joined.

Proof:

               Statements                        Reasons

1.    OT = OS -----------------> Radii of the same circle.

2.    OS < OR -----------------> OS is a part of OR.

3.    OT < OR -----------------> From statements 1 and 2.

4.    OT is the shortest length of all the lines drawn from O to PQ ------> It is true for every line joining O to PQ.

5.    OT ⊥ PQ ------> Perpendicular is the shortest line segment drawn from a point to a line.

                                                                              Proved.

2.   The length of two tangents drawn from an external point to a circle are always equal.

Given: O is the centre of a circle. PQ and PR are two tangents from the same point P to the circle at T1 and T2.

To Prove: PT₁ = PT₂

Construction: OP, OT₁ and OT₂ are joined.

Proof:

              Statements                            Reasons

1.    In DOPT₁ and DOPT₂

i.       ∠OT₁P = ∠OT₂P (R) -------> Both of them are right angles.

ii.     OP = OP (H) ---------------> Common side.

iii.    OT₁ = OT₂ (S) ------------> Radii of the same circle.

2.    DOPT₁ ≅ DOPT₂ ----------------> By RHS axiom.

3.    PT₁ = PT₂ ---------> Corresponding sides of congruent triangles.

                                                                              Proved.

 

3.   The alternate segment angles are always equal.

Given: O is the centre of a circle. PQ is a tangent to the circle at point of contact T. TA is a chord. ∠ATP and ∠TBA; ∠ATQ and ∠TCA are two pair of alternate segment angles.

To Prove: ∠ATP = ∠TBA and ∠ATQ = ∠TCA

Construction: OT joined and TO is produced to R, a point on the circumference. Hence, TR is the diameter of the circle. RA is joined.

Proof:

              Statements                        Reasons

1.    ∠RAT = 90° --------------> Angle in the semi-circle.

2.    ∠RTA + ∠TRA = 90° -----> Sum of two acute angles of a rt. angled DRAT.

3.    ∠RTA + ∠ATQ = 90° -----> RT ⊥ PQ

4.    ∠RTA + ∠TRA = ∠RTA + ∠ATQ ------> From statements 2 and 3.

i.e. ∠TRA = ∠ATQ

5.    ∠TRA = ∠TCA ----------> Inscribed angles on same arc ABT.

6.    ∠TCA = ∠ATQ ------------> From statements 4 and 5.

7.    Similarly, ∠ATP = ∠TBA ---------> Same facts and reasons as above.

                                                                              Proved.

Look at the following worked out examples on tangents of a circle:

 

Workout Examples

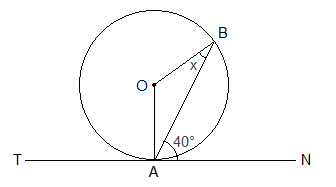
Example 1: In the given figure, O is the centre of circle. TAN is a tangent to the circle where A is the point of contact. If ∠BAN = 40° and ∠ABO = x°, find the value of x.

Solution: Here,

                   ∠BAN = 40°

                   ∠OAN = 90° [∵ OA ⊥ TN]

                   ∠OAN = ∠OAB + ∠BAN [∵ Whole part axiom]

         i.e.     90° = ∠OAB + 40°

         or,     ∠OAB = 90° - 40°

         or,     ∠OAB = 50°

                  ∠ABO = ∠OAB = 50° [∵ OA = OB]

             ∴        x = 50° 

 

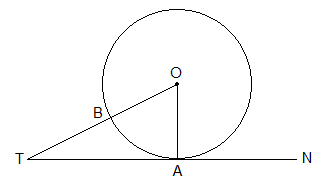
Example 2: In the given fugure, O is the centre of circle. TAN is a tangent to the circle at A where A is the point of contact. If OA = 8cm and AT = 15cm, find the length of BT.

Solution: Here,

                   AT = 15cm, OA = 8cm, BT = ?

                   ∠OAT = 90° [∵ OA ⊥ TN]

                   ∴ DOAT is a right angled triangle

                   OT² = OA² + AT² [∴ Pythagoras relation]

          i.e.     OT² = 8² + 15²

          or,     OT² = 64 + 225

          or,     OT² = 289

          or,     OT = √289 = 17cm

          Now,

          BT = OT – OB

               = OT – OA [∵ OA = OB, radii of same circle]

               = 17cm – 8cm

               = 9cm

Example 3: In the given figure, O is the centre of a circle. TAN is a tangent to the circle at A. If ∠ACB = 65° and ∠CAT = x°, find the value of x.

Solution: From the figure,

                  ∠CAB = 90° [∵ Inscribed angle on semi-circle]

                  ∠CAB + ∠ACB + ∠ABC = 180° [Sum of angles of DABC]

        i.e.     90° + 65° + ∠ABC = 180°

        or,     155° + ∠ABC = 180°

        or,     ∠ABC = 180° - 155°

        or,     ∠ABC = 25°

           

          ∠CAT = ∠ABC [∵ Angles in the alternate segments]

          ∴ x = 25° 

 

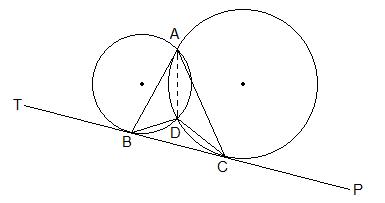
Example 4: In the adjoining figure, two circles intersect each other at A and D. Their common tangent TP meets the two circles at B and C. Prove that, ∠BAC + ∠BDC = two right angles.

Solution:

Given: Two circles intersect each other at A and D. TP is a common tangent at B and C.

To Prove: ∠BAC + ∠BDC = 180°

Construction: Points A and D are joined.

Proof:

      Statements                                 Reasons

1.   ∠DAB = ∠DBC -----> Being angles in the alternate segment of the circle.

2.   ∠DAC = ∠DCB -----> By reason similar to 1.

3.   ∠DAB + ∠DAC = ∠DBC + ∠DCB -----> By adding statements 1 and 2.

i.e. ∠BAC = ∠DBC + ∠DCB

4.   ∠DBC + ∠DCB + ∠BDC = 180° ------> Sum of angles of DDBC.

5.   ∠BAC + ∠BDC = 180° ------> From statements 3 and 4.

                                                                                      Proved.

Example 5: In the given figure, PQ is a tangent to the circle at point of contact A. C is the middle point of arc AB. If CM ⊥ PQ and CN ⊥ AB, prove that CM = CN.

Solution:

Given: O is the centre of circle. PQ is a tangent to the circle at point of contact A. C is the mid-point of arc ACB i.e. arc AC = arc BC, CM ⊥ PQ and CN ⊥ AB.

To Prove: CM = CN

Construction: AC and BC joined.

Proof:

       Statements                                 Reasons

1.   Chord AC = chord BC ---------> being arc AC = arc BC.

2.   ∠BAC = ∠ABC --------------> Being AC = BC in DABC.

3.   ∠CAM = ∠ABC ---------------> Alternate segment angles of a circle.

4.   ∠BAC = ∠CAM ----------------> From statements 2 and 3.

5.   In DACM and DACN

i.        ∠AMC = ∠ANC (A) --------> Both being 90°.

ii.      ∠CAM = ∠CAN (A) -------> From statement 4.

iii.     AC = AC (S) -------> Common side.

6.   DACM ≅ DACN -----------> By AAS axiom.

7.   CM = CN -------------> Corresponding sides of ≅ triangles.

                                                                                       Proved.

 

You can comment your questions or problems regarding circle and tangents here.