
Cyclic Quadrilateral
A quadrilateral having its all four vertices on the circumference of a circle is called a cyclic quadrilateral.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
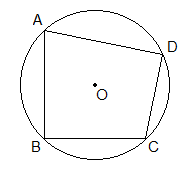
ABCD, in the given figure, is a cyclic quadrilateral.
Concyclic Points
The points lying on the circumference of the circle are called concyclic points.

In the given circle, A, B, C, D are concyclic points.
Theorems on Cyclic Quadrilateral and Their Proofs:
THEOREM 1:
The sum of opposite angles of a cyclic quadrilateral is always
180°.
PROOFS:

Given: PQRS is a cyclic
quadrilateral.
To Prove: (i) ∠QPS + ∠QRS = 180°
(ii) ∠PQR + ∠PSR = 180°
Proof:
Statements Reasons
1.
∠QPS = ½ Arc QRS -----> Inscribed
angle is equal to the half of its opposite arc.
2.
∠QRS = ½ Arc QPS ----->
Inscribed angle is equal to half of its opposite arc.
3.
∠QPS + ∠QRS = ½ Arc QRS + ½ Arc QPS -----> Adding statements 1 and 2.
or, ∠QPS + ∠QRS = ½ Arc (QRS + QPS)
or, ∠QPS + ∠QRS = ½ Circle PQRS
or, ∠QPS + ∠QRS = ½ 360°
or, ∠QPS + ∠QRS = 180°
4.
∠PQR + ∠PSR = 180° -----> Same as above.
Hence proved.
THEOREM 2:
In a cyclic quadrilateral, the exterior angle is equal to its
opposite interior angle.
PROOFS:
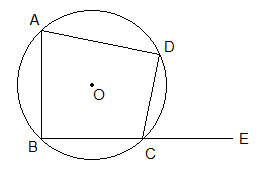
Given: ABCD is a cyclic
quadrilateral with exterior angle ∠DCE.
To Prove: ∠DCE = ∠BAD
Proof:
Statements Reasons
1.
∠DCE + ∠BCD = 180° -----> Opposite angles of a cyclic quadrilateral
are supplementary.
2.
∠BAD + ∠BCD = 180° -----> Linear pair of angles.
3.
∠DCE + ∠BCD = ∠BAD + ∠BCD -----> From statements 1 and 2.
4.
∠DCE = ∠BAD -----> Cancelling common angle ∠BCD.
Hence proved.
Problems on Cyclic Quadrilaterals
Worked Out Examples
Example 1: Find ∠COD in the given figure.

Solution: From the figure,
110° + ∠ODC = 180° [Opposite
angles of a cyclic quadrilateral]
or, ∠ODC = 180° – 110°
or, ∠ODC = 70°
∠ODC = ∠OCD = 70° [Being OC = OD,
radii of same circle]
∠COD + ∠ODC + ∠OCD = 180° [Sum of angles of DCOD]
or, ∠COD + 70° + 70° = 180°
or, ∠COD + 140° = 180°
or, ∠COD = 180° – 140°
or, ∠COD = 40° Ans.
Example 2: Calculate the value of x and y in the given figure.
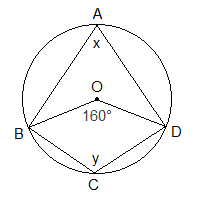
Solution: From the figure,
x = ½ ∠BOD [Inscribed
angle is half of central angle]
or, x = ½ 160°
or, x = 80°
y + x = 180° [Opposite
angles of a cyclic quadrilateral]
or, y + 80° = 180°
or, y = 180° – 80°
or, y = 100°
Hence, x = 80° and y = 100°
Ans.
Example 3: Find the angle x in the given figure.

Solution: From the figure,
∠CAD = 56° [Inscribed angle on same arc CD]
∠BAD = 96° [Exterior angle of a cyclic quadrilateral]
Now,
x = ∠BAD – ∠CAD
= 96° – 56°
= 40°
Ans.
Example 4: In the adjoining figure, ABCD is a cyclic quadrilateral, side CD is
produced to the point E, where BC = DE. If CA bisects ∠BCD prove that DACE is an
isosceles triangle.
Solution: Here,
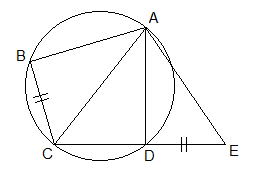
Given: ABCD is a cyclic
quadrilateral. BC = DE and ∠BCA = ∠ACD.
To Prove: DACE is an isosceles triangle.
Proof:
Statements Reasons
1. ∠BCA = ∠ACD -----> Given.
2. Arc AB = arc AD -----> Arcs subtended by equal inscribed angles.
3. AB =AD ------> Equal chords cut off equal arcs in a circle.
4. In DABC
and DADE
i. AB = AD (S) -----> From statement 3
ii. ∠ABC = ∠ADE (A) -----> Exterior
angle of a cyclic quadrilateral
iii. BC = DE (S) -----> Given.
5. DABC ≅ DADE
-----> By SAS axiom
6. AC = AE -----> Corresponding sides of ≅ triangles.
7. ACE is an isosceles triangle -----> Being AC = AE.
Hence proved.
Example 5: In the given figure, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = SR.
Solution: Here,

Given: PQRS is a cyclic
quadrilateral. ∠RPS = ∠SPT.
To Prove: SQ = SR.
Proof:
Statements Reasons
1.
∠SPT = ∠RPS -----> From given.
2.
∠SPT = ∠QRS -----> Exterior angle of cyclic quadrilateral PQRS.
3.
∠SQR = ∠RPS -----> Inscribed angle on same arc RS.
4.
∠SQR = ∠QRS -----> From statements 1, 2 and 3.
5.
SQ = SR -----> Being
base angles of DSQR
equal, statement 4.
Hence proved.
If you have any question or problems regarding the Cyclic
Quadrilaterals, you can ask here, in the comment
section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: