Addition Law of Probability
If A and B are two mutually exclusive or non-exclusive events then the occurrence of at least one event A or B (i.e. A∪B) in a single trial is given by the following laws of addition of probabilities.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Addition law of probability of mutually exclusive events:
Two or more events of a sample space S are said to be mutually exclusive if the occurrence of any one event excludes the occurrence of the other events. For example, let's consider the experiment of throwing a dice. Let A be the event, ‘the number obtained is less than 5’. Then, A = {1, 2, 3, 4}. Again, B be the event, ‘the number obtained is at least 5’. Then, B = {5, 6}. Here A∩B = φ, i.e the joint occurrence of A and B is impossible, i.e. occurrence of A excludes the occurrence of B. So, the events A and B are mutually exclusive.
If A and B are any two mutually exclusive events of a sample space S, i.e. A∩B = φ, the probability of occurrence of either A or B (i.e. A∪B) in a single trial is equal to the sum of the individual probabilities of the occurrence of A and B.
i.e. P(A or B) = P(A) + P(B)
i.e. P(A∪B)
= P(A) + P(B)
Further more, if A, B and C are three mutually
exclusive events, then,
P(A
or B or C) = P(A∪B∪C)
= P(A) + P(B) + P(C)
and
so on.
Addition law of probability of non-mutually exclusive events:
Two or more events of a sample space S are said to be non-mutually exclusive if the occurrence of any one event does not excludes the occurrence of the other events. For example, let’s consider the experiment of throwing a dice. Let A be the event ‘the number obtained is even’ and B be the event ‘the number obtained is less than 4’. Then, A = {2, 4, 6} and B = {1, 2, 3} and ∴ A∩B = {2}. It means, the events A and B can occur simultaneously in a single throw of a dice. So they are non-mutually exclusive events.
If A and B are any two non-mutually exclusive events of a sample space S, i.e. A∩B ≠ φ, then the probability of occurrence of either A or B (i.e. A∪B) in a single trial is given by,
P(A or
B) = P(A∪B)
= P(A) + P(B) – P(A∩B)
Worked out examples on addition law of probabilities:
Example 1: One card is drawn at random from the numbered cards,
numbered from 10 to 21. Find the probability that the card may be prime
numbered or even numbered card.
Solution:
Let n(S) be
the exhaustive cases, n(A) be the number of events of prime numbered cards and
n(B) be the number of events of even numbered cards. Then,
S = {10,
11, 12, ………, 21}
∴ n(S) = 12
A = {11,
13, 17, 19}
∴ n(A) = 4
B = {10,
12, 14, 16, 18, 20}
∴ n(B) = 6
Now,
P(A) =
n(A)/n(S) = 4/12 = 1/3
P(B) =
n(B)/n(S) = 6/12 = ½
By using the
law of addition of probabilities of mutually exclusive events,
P(A or
B) = P(A∪B) = P(A) + P(B) = 1/3 + ½ = 5/6
So, the
probability that the card may be prime numbered or even numbered is 5/6.
Example 2: From a pack of 52 cards, a card is drawn at random. What
is the probability of getting a card with face or an ace?
Solution:
Let n(S) be
the exhaustive cases, n(A) the number of events of face card and n(B) the
number of events of ace. Then,
n(S) =
52
n(A) =
12
n(B) = 4
Now, by
using the law of addition of probabilities of mutually exclusive events,
P(A or B)
= P(A∪B)
= P(A) + P(B)
= n(A)/n(S) + n(B)/n(S)
= 12/52 + 4/52
= 16/52
= 4/13
Hence, the
probability that the card may be a face card or an ace is 4/13.
Example 3: A bag contains 3 red, 5 blue, 7 black and 9 white
identical balls. If a ball is drawn randomly from the bag, find the probability
that it may be either red or blue or white.
Solution:
Let n(S) be
the exhaustive cases, n(A) the number of cases of red balls, n(B) the number of
cases of blue balls and n(C) the number of cases of white balls. Then,
n(S) = 3
+ 5 + 7 + 9 = 24
n(A) = 3
n(B) = 5
n(C) = 9
n(S) =
5+7 = 12
Now, by
using the law of addition of probabilities of mutually exclusive events,
P(A or B
or C) = P(A∪B∪C) = P(A) + P(B) + P(C)
= n(A)/n(S) + n(B)/n(S) + n(C)/n(S)
= 3/24 + 5/24 + 9/24
= 17/24
Hence, the
probability that the ball may be either red or blue or white is 17/24.
Example 4: From the pack of 52 playing cards, a card is drawn
randomly. Find the probability of getting it red or face card.
Solution:
Let n(S) be
the exhaustive cases, n(A) be the number of events of red card and n(B) be the
number of events of face cards. Then,
n(S) =
52
n(A) =
26
n(B) =
12
Since there
are 6 face cards which are red (3 face cards of heart + 3 face cards of
diamond),
n(A∩B) = 6
Now, by
using the law of addition of probabilities of non-mutually exclusive events,
P(A or
B) = P(A∪B)
= P(A) + P(B) – P(A∩B)
= n(A)/n(S) + n(B)/n(S) – n(A∩B)/n(S)
= 26/52 + 12/52 – 6/52
= (26 + 12 – 6)/52
= 32/52
= 8/13
Hence, the probability of getting red
or face card is 8/13.
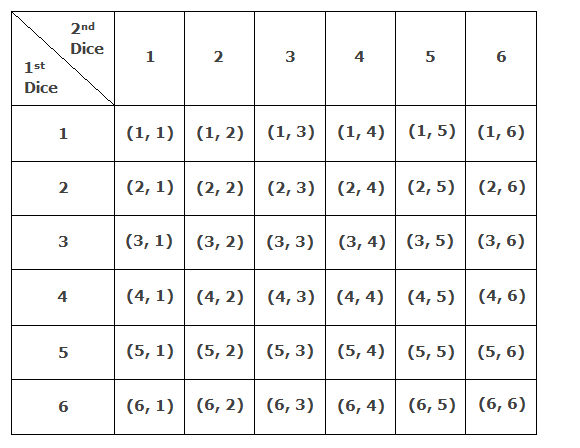
Example 5: Two unbiased dice are rolled. Find the probability that
the sum of the numbers on the two faces is either divisible by 3 or divisible
by 4.
Solution:
Two dice can
be thrown in 36 ways as given in the table below.
Let n(S) be
the exhaustive cases, n(A) the number of events that the sum is divisible by 3
and n(B) the number of events that the sum is divisible by 4. Then,
n(S) = 36
A = {(1, 2),
(2, 1), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (3, 6), (4, 5), (5, 4), (6, 3),
(6,6)}
∴ n(A) = 12
B = {(1, 3),
(2, 2), (3, 1), (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (6, 6)}
∴ n(B) = 9
The event A∩B happens when the sum
is divisible by 3 as well as 4, i.e. the sum is 12 which is (6, 6).
∴ n(A∩B) = 1
Now, by using
the law of addition of probabilities of non-mutually exclusive events,
P(A or
B) = P(A∪B)
= P(A) + P(B) – P(A∩B)
= n(A)/n(S) + n(B)/n(S) – n(A∩B)/n(S)
= 12/36 + 9/36 – 1/36
= (12 + 9 – 1)/36
= 20/36
= 5/9
Hence, the
probability that the sum of the numbers on the two faces is either divisible by
3 or 4 is 5/9
You can comment your questions or problems regarding the addition law of probability here.




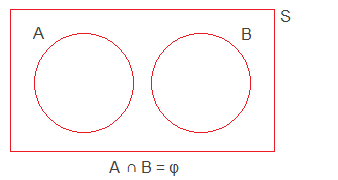

0 comments: