Multiplication and division of algebraic fractions

0 comments

Multiplication and division of algebraic fractions

Multiplication and division of algebraic fractions

Multiplication of algebraic fractions: In the case of multiplication of monomial algebraic fractions, we should multiply the numerators and denominators separately. Then, the product is reduced to the lowest terms by using the laws of indices. For example,



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************

Example of multiplication of monomial algebraic fractions

In the case of multiplication of polynomial algebraic fractions, the numerators and denominators are factorized. Then, they are reduced to their lowest terms. For example,        

Example of multiplication of polynomial algebraic fractions

Division of algebraic fractions: In the case of division of algebraic fractions, we should multiply the dividend by the reciprocal of the divisor as like the process of multiplication of algebraic fractions. For example,       

Examples of division of algebraic fractions

Look at the following worked out examples:

Workout Examples

Example 1: Simplify: (i) (3a^2)/(5b^2 ) × (15ab^3)/(27a^2 ) (ii) 2x/(2x+y) × 〖2xy+y〗^2/(8y^3 )

Solution: 1(i) (3a^2)/(5b^2 )× (15ab^3)/(27a^2 ) = (45a^3 b^3)/(135a^2 b^2 ) = ab/3

Solution: 1(ii) 2x/(2x+y) × 〖2xy+y〗^2/(8y^3 ) = 2x/(2x+y) × (y(2x+y))/(8y^3 ) = (2xy(2x+y))/(8y^3 (2x+y)) = x/(4y^2 )


Example 2: Simplify: (i) (a^2+ ab)/(a^2- ab) × (ab-〖 b〗^2)/(a^2-b^2 ) (ii) (x^2-9)/(x^2+4x) × (x^2+ 2x-8)/(x^2+ x - 6)

Solution: 2(i) (a^2+ ab)/(a^2- ab) × (ab-〖 b〗^2)/(a^2-b^2 ) = (a(a+b))/(a(a-b)) × (b(a-b))/((a+b)(a-b)) = b/(a-b)


Solution: 2(ii) (x^2-9)/(x^2+4x) × (x^2+ 2x-8)/(x^2+ x - 6) = (x^2-3^2)/(x(x+4)) × (x^2+ 4x-2x-8)/(x^2+ 3x-2x - 6) = ((x+3)(x-3))/(x(x+4)) × (x(x+4) -2(x+4))/(x(x+3) -2(x+3)) = ((x+3)(x-3))/(x(x+4)) × ((x+4)(x-2))/((x+3)(x-2)) = (x-3)/x

Example 3: Simplify: (3x^2)/(x+2) × 2/(x-2)× (x^2-4)/(15x^2 y)

Solution: (3x^2)/(x+2) × 2/(x-2)× (x^2-4)/(15x^2 y) = (3x^2)/(x+2) × 2/(x-2)× (x^2-2^2)/(15x^2 y) = (3x^2)/(x+2) × 2/(x-2)× ((x+2)(x-2))/(15x^2 y) = 2/5y

Example 4: Simplify: (i) (3a^2 b)/4xy ÷ (6ab^2)/(8xy^2 ) (ii) (x^2-y^2)/xy ÷ (x-y)/y^2

Solution: 4(i) (3a^2 b)/4xy ÷ (6ab^2)/(8xy^2 ) = (3a^2 b)/4xy × (8xy^2)/(6ab^2 ) = (24a^2 bxy^2)/(24xyab^2 ) = ay/b

Solution: 4(ii) (x^2-y^2)/xy ÷ (x-y)/y^2 = (x^2-y^2)/xy × y^2/(x-y) = ((x+y)(x-y))/xy × y^2/(x-y) = (y(x+y))/x


Example 5: Simplify: (i) (3x^2-4x-7)/(x^2-1) ÷ (3x^2-7x)/(x+1) (ii) (2x/(x-1) ÷ (x+1)/1) ÷ 2/(x^2-1)

Solution: 5(i) (3x^2-4x-7)/(x^2-1) ÷ (3x^2-7x)/(x+1) = (3x^2-4x-7)/(x^2-1) × (x+1)/(3x^2-7x) = (3x^2-7x+3x-7)/(x^2-1^2 ) × (x+1)/(x(3x-7)) = (x(3x-7) +1(3x-7))/((x+1)(x-1)) × (x+1)/(x(3x-7)) = ((3x-7)(x+1))/((x+1)(x-1)) × (x+1)/(x(3x-7)) = ((x+1))/(x(x-1))

Solution: 5(ii) (2x/(x-1) ÷ (x+1)/1) ÷ 2/(x^2-1) = (2x/(x-1) × 1/(x+1)) × (x^2-1)/2 = 2x/(x-1) × 1/(x+1) × (x^2-1^2)/2 = 2x/(x-1) × 1/(x+1) × ((x+1)(x-1))/2 = x


Example 6: Simplify: (x^2+3x+2)/(x^2-4x-12) ÷ (x^2-x-6)/(x^2-9x+18)

Solution: (x^2+3x+2)/(x^2-4x-12) ÷ (x^2-x-6)/(x^2-9x+18) = (x^2+3x+2)/(x^2-4x-12) × (x^2-9x+18)/(x^2-x-6) = (x^2+2x+x+2)/(x^2-6x+2x-12) × (x^2-6x-3x+18)/(x^2-3x+2x-6) = (x(x+2) +1(x+2))/(x(x-6) +2(x-6)) × (x(x-6) -3(x-6))/(x(x-3) +2(x-3)) = ((x+2)(x+1))/((x-6)(x+2)) × ((x-6)(x-3))/((x-3)(x+2)) = (x+1)/(x+2)

Example 7: Simplify: (x-4)/(x+4) × (x-3)/(x+4) ÷ (x^2-7x+12)/(x^2+7x+12)
Solution: (x-4)/(x+4) × (x-3)/(x+4) ÷ (x^2-7x+12)/(x^2+7x+12) = (x-4)/(x+4) × (x-3)/(x+4) × (x^2+7x+12)/(x^2-7x+12) = (x-4)/(x+4) × (x-3)/(x+4) × (x^2+3x+4x+12)/(x^2-3x-4x+12) = (x-4)/(x+4) × (x-3)/(x+4) × (x(x+3) +4(x+3))/(x(x-3) -4(x-3)) = (x-4)/(x+4) × (x-3)/(x+4) × ((x+3)(x+4))/((x-3)(x-4)) = (x+3)/(x+4)


You can comment your questions or problems regarding multiplication and division of algebraic fractions here.


Labels:

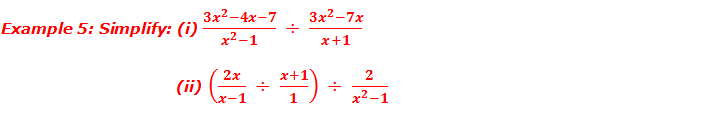
0 comments:

Subscribe to: Post Comments (Atom)