Arcs and Angles Subtended by Arcs on a Circle

Arcs and Angles Subtended by Arcs on a Circle

A portion (part) of the circumference of a circle is called an arc. In the figure given below, ACB is a part of the circumference of the circle with centre O. So ACB is an arc. There are minor arcs and major arcs. A minor arc is less than the half of the circumference and major arc is greater than the half of the circumference.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

So, arc ACB is a minor arc and the arc ADB is a major arc.

 

Central angle and its corresponding arc

In the figure given below, O is the centre of the circle in which OP and OQ are two radii and PRQ is an arc. The arc PRQ subtends an angle POQ at the centre O. So, ∠POR is called the central angle and the arc PRQ is its corresponding arc.

Since both the central angle and corresponding arc are described by the same amount of rotation, therefore the degree measure of arc PRQ and ∠POQ are same.

i.e. ∠POQ ≗ arc PRQ 

Inscribed angle and its corresponding arc

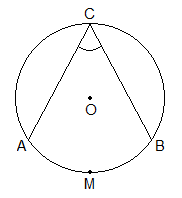
In the figure given below, O is the centre of the circle in which AB and BC are two chords. The chords AB and BC meet at a point B on the circumference of the circle. So they form an angle ABC at B on the circumference. 

The angle on the circumference is called the inscribed angle. So, ∠ABC is an inscribed angle and arc AMC is its corresponding arc.

Now, to understand and establish the relation between an inscribed angle and its corresponding arc, let us consider an example of the figure given below:

In DAOB, ∠OAB = ∠OBA [∵ OA = OB]

          ∠OAB + ∠OBA + ∠AOB = 180° [Sum of angles of a triangle]

or,      ∠OBA + ∠OBA + ∠AOB = 180°

or,      2∠OBA = 180° - ∠AOB ………………. (i)

In DBOC, ∠OBC = ∠OCB [∵ OB = OC]

          ∠OBC + ∠OCB + ∠BOC = 180° [Sum of angles of a triangle]

or,      ∠OBC + ∠OBC + ∠BOC = 180°

or,      2∠OBC = 180° - ∠BOC ………………. (ii)

Adding (i) and (ii), we have

2∠OBA + 2∠OBC = 180° - ∠AOB + 180° - ∠BOC

or,      2(∠OBA + ∠OBC) = 360° - (∠AOB + ∠BOC)

or,      2∠ABC = 360° - Reflex ∠AOC

or,      2∠ABC ≗ circumference – arc ABC [∵ Circumference ≗ 360° and Ref.∠AOC ≗ arc ABC]

or,      2∠ABC ≗ arc AMC

or,      ∠ABC ≗ ½ arc AMC

Thus, the degree measurement of the angle on circumference of a circle is equal to the half of the degree measurement of its corresponding arc.

Properties of circle related to arcs and the angles subtended by them:

1.    Arcs subtended by equal angles at the centre of the circle are equal.

2.    Angles subtended by two equal arcs of a circle at the centre are equal.

3.    Arcs cut off by equal chords of a circle are equal. Or, If two chords of a circle are equal, the corresponding arcs are equal.

4.    If two arcs of a circle are equal, then their corresponding chords are equal.

5.    Central angle of a circle is equal to the degree measurement of its opposite arc.

6.    Inscribed angle of a circle is equal to the half of the degree measurement of its opposite arc.

7.    Degree measurement of a full circle arc is equivalent to 360°.

For more on central angles, inscribed angles and theorems related to them, visit to the page: Circle Theorems on Central Angles and Inscribed Angles.