Proportional

0 comments

Proportional

Proportional

If two ratios are equal then they are said to be in proportion or proportional. If a/b = c/d, it is written as a:b::c:d and read as ‘a’ is to ‘b’ is as ‘c’ is to ‘d’. The first term ‘a’ and the fourth term ‘d’ are called extremes and second term ‘b’ and third term ‘c’ are called means.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************

Extremes and means

If a:b = b:c = c:d i.e. a/b = b/c = c/d then the terms a, b, c, d are said to be in continued proportion.

If a/b = b/c then b2 = ac. Thus three quantities are said to be in continued proportion if the product of extremes is equal to the square of mean.

 

Properties of proportion

If a, b, c and d are four numbers then,

1.   Invertendo:

Invertendo

             This property is called as invertendo.

 

2.   Alternendo:

Alternendo
                This property is called as Alternendo.

 

3.   Componendo:

Componendo

             This property is called as componendo.

 

4.   Dividendo:

Dividendo

             This property is called as dividendo.

 

5.   Componendo and dividendo:

Componendo and dividendo

             This property is called componendo and dividendo.

 

6.   Convertendo or subtendo:

Convertendo or subtendo

             This property is called convertendo or subtendo.

 

7.   Addendo:

Addendo
                This property is called addendo.

Some problems on proportional and their solutions:

Example 1: If 5, 10, 15 are in proportion, find the fourth proportion.

Solution: Let x be the fourth proportion. Then 5, 10, 15 and x are in proportion.        

5, 10, 15 and x are in proportion

 

Example 2: If 2, x, 6 and 12 are in proportion, find the value of x.

Solution: Here, 2, x, 6 and 12 are in proportion.          

2, x, 6 and 12 are in proportion

 

Example 3: 4, x and 9 are in continued proportion, find the value of x.

Solution: Here, 4, x, 9 are in continued proportion.          

4, x, 9 are in continued proportion

Example 4: What number should be added to each of the numbers 2, 4, 8 and 12 to make them proportional?

Solution: Let the required number be a.          

Let, a should be added to make them proportional

 

Example 5: If a/b=c/d then prove that (a^2+b^2)/(c^2+d^2 ) = ((a+b)/(c+d))^2.


Example 6: If a/b=c/d= e/f then prove that (a^3+c^3+e^3)/(b^3+d^3+f^3 ) = ace/bdf.

 

Example 7: If (x+3y+2z+6a)/(x+3y-2z-6a)=(x-3y+2z-6a)/(x-3y-2z+6a) , prove that x/y = z/a


Example 8: If a, b, c are in continued proportion, prove that 1/a^3 +1/b^3 +1/c^3 = (a^3+b^3+c^3)/(a^2 b^2 c^2 ).

advertisement6

Example 9: If a, b, c and d are in continued proportion, prove that: √ab-√bc+√cd= √((a-b+c)(b-c+d))

advertisement7

Example 10: If a, b, c and d are in continued proportion, prove that: a/d=(a^3+b^3+c^3)/(b^3+c^3+d^3 )

 

You can comment your questions or problems regarding the proportional here.


Labels:

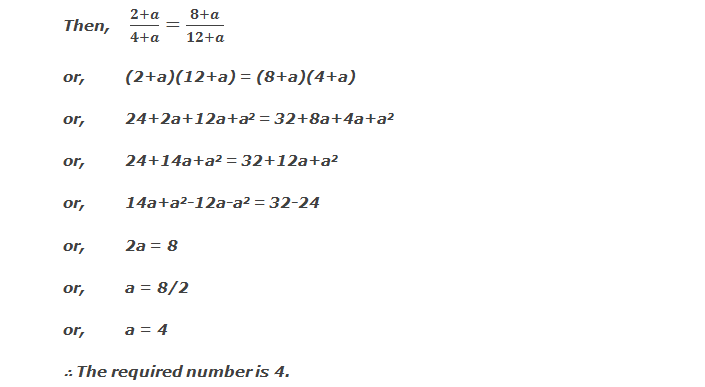
0 comments:

Subscribe to: Post Comments (Atom)