Laws of Indices

4 comments

Laws of indices banner

 

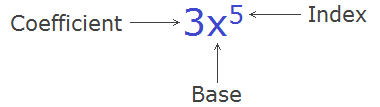
'Indices' is the plural form of 'index'. And, index means the power of any number or variable term, which is called a base. Power or index is also known as an exponent.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver



********************


Install 10 Math Problems




********************



Coefficient, base and index

 

There are certain rules which are used to solve the problems of indices. These rules are called the laws of indices. Some laws of indices are as follows: 



Laws of Indices


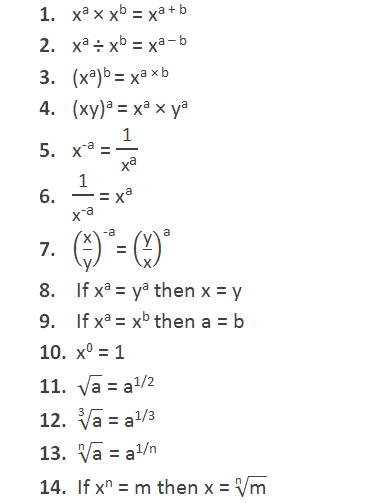
Law’s of indices: 1) xa × xb = xa + b 2) xa ÷ xb = xa – b 3) (xa)b = xa × b 4) (xy)a = xa × ya 5) "x" ^"-a" = "1" /〖" x" 〗^"a" 6) "1" /"x" ^"-a" = "x" ^"a" 7) ("x" /"y" )^"-a" = ("y" /"x" )^"a" 8) If xa = ya then x = y 9) If xa = xb then a = b 10) x0 = 1 11) √("a" ) = a1/2 12) √("3" &"a" ) = a1/3 13) √("n" &"a" ) = a1/n 14) If xn = m then x = √("n" &"m" )

Problems involving laws of indices


Example 1: Find the value of: 274/3

 

Solution:

 

Here, 

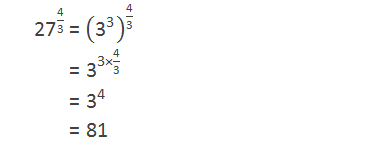
〖"27" 〗^("4" /"3" ) = ("3" ^"3" )^("4" /"3" ) = "3" ^("3×" "4" /"3" ) = "3" ^"4" = "81"


Example 2: Find the value of: (2401)-1/4

 

Solution:

 

Here,

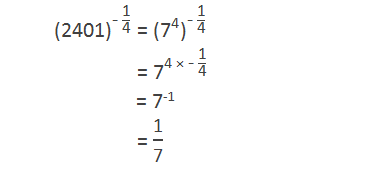
〖"(2401)" 〗^("- " "1" /"4" ) = 〖"(" "7" ^"4" ")" 〗^("- " "1" /"4" ) = "7" ^("4 × - " "1" /"4" ) = 7-1 = "1" /"7"

Example 3: Find the value of: 

[√("3" &"64" ) " ÷ " ("1" /"125" )^("-1" /"3" ) ]^"2"

 

Solution:

 

Here,

[√("3" &"64" ) " ÷ " ("1" /"125" )^("-1" /"3" ) ]^"2" = ["4" ^("3 ×" "1" /"3" ) " ÷ " ("125" )^("1" /"3" ) ]^"2" = ["4 ÷ " "5" ^("3 × " "1" /"3" ) ]^"2" = ["4 ÷ 5" ]^"2" = ["4" /"5" ]^"2" = "16" /"25"

       

Example 4: Find the value of: 

("81" /"16" )^("-3" /"4" ) " × " [("25" /"9" )^("-3" /"2" ) " ÷ " ("5" /"2" )^"-3" ]


Solution:

 

Here,

("81" /"16" )^("-3" /"4" ) " × " [("25" /"9" )^("-3" /"2" ) " ÷ " ("5" /"2" )^"-3" ] = ("16" /"81" )^("3" /"4" ) " × " [("9" /"25" )^("3" /"2" ) " ÷ " ("2" /"5" )^"3" ] = ("2" /"3" )^("4 × " "3" /"4" ) " × " [("3" /"5" )^("2 × " "3" /"2" ) " ÷ " "8" /"125" ] = ("2" /"3" )^"3" " × " [("3" /"5" )^"3" " × " "125" /"8" ] = "8" /"27" " ×" "27" /"125" " × " "125" /"8" = 1

 Example 5: Find the value of: 

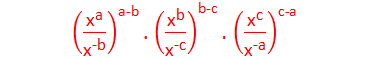
("x" ^"a" /"x" ^"-b" )^"a-b" " ." ("x" ^"b" /"x" ^"-c" )^"b-c" "." ("x" ^"c" /"x" ^"-a" )^"c-a"


Solution:

 

Here, 

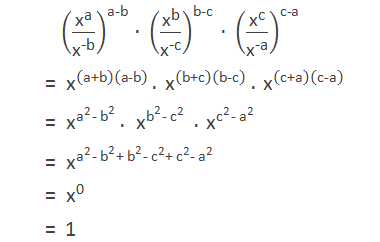
= ("x" ^"a" /"x" ^"-b" )^"a-b" × ("x" ^"b" /"x" ^"-c" )^"b-c" × ("x" ^"c" /"x" ^"-a" )^"c-a" = "x" ^("a+b" )"(a-b)" × "x" ^("b+c" )"(b-c)" × "x" ^("c+a" )"(c-a)" = "x" ^("a" ^"2" "-" 〖" b" 〗^"2" ) × "x" ^("b" ^"2" "- " "c" ^"2" ) × "x" ^("c" ^"2" "-" 〖" a" 〗^"2" ) = "x" ^("a" ^"2" "- " "b" ^"2" "+ " "b" ^"2" "- " "c" ^"2" "+ " "c" ^"2" "- " "a" ^"2" ) = "x" ^"0" = 1

 


Example 6: Simplify: 

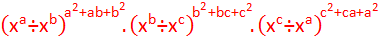
("x" ^"a" "÷" "x" ^"b" )^("a" ^"2" "+ab+" "b" ^"2" ).("x" ^"b" "÷" "x" ^"c" )^("b" ^"2" "+bc+" "c" ^"2" ).("x" ^"c" "÷" "x" ^"a" )^("c" ^"2" "+ca+" "a" ^"2" )


Solution:

 

Here,         

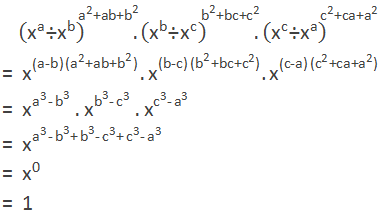
= ("x" ^"a" "÷" "x" ^"b" )^("a" ^"2" "+ab+" "b" ^"2" ).("x" ^"b" "÷" "x" ^"c" )^("b" ^"2" "+bc+" "c" ^"2" ).("x" ^"c" "÷" "x" ^"a" )^("c" ^"2" "+ca+" "a" ^"2" ) = "x" ^(("a-b" )"(" "a" ^"2" "+ab+" "b" ^"2" ")" )."x" ^(("b-c" )"(" "b" ^"2" "+bc+" "c" ^"2" ")" ) "." "x" ^(("c-a" )"(" "c" ^"2" "+ca+" "a" ^"2" ")" ) = "x" ^("a" ^"3" "-" "b" ^"3" ) " × " "x" ^("b" ^"3" "-" "c" ^"3" ) " × " "x" ^("c" ^"3" "-" "a" ^"3" ) = "x" ^("a" ^"3" "-" "b" ^"3" "+" "b" ^"3" "-" "c" ^"3" "+" "c" ^"3" "-" "a" ^"3" ) = "x" ^"0" = 1 

Example 7: Simplify: 

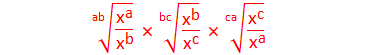
√("ab" &"x" ^"a" /"x" ^"b" ) " × " √("bc" &"x" ^"b" /"x" ^"c" ) " × " √("ca" &"x" ^"c" /"x" ^"a" )


Solution:

 

Here, 

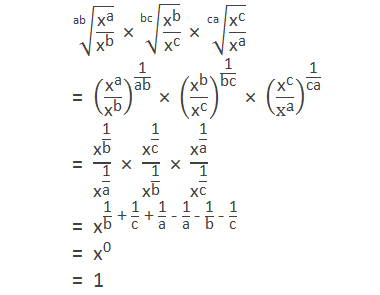
√("ab" &"x" ^"a" /"x" ^"b" ) " × " √("bc" &"x" ^"b" /"x" ^"c" ) " × " √("ca" &"x" ^"c" /"x" ^"a" ) = ("x" ^"a" /"x" ^"b" )^("1" /"ab" ) " × " ("x" ^"b" /"x" ^"c" )^("1" /"bc" ) " × " ("x" ^"c" /"x" ^"a" )^("1" /"ca" ) = "x" ^("1" /"b" )/"x" ^("1" /"a" ) " × " "x" ^("1" /"c" )/"x" ^("1" /"b" ) " × " "x" ^("1" /"a" )/"x" ^("1" /"c" ) = "x" ^("1" /"b" " + " "1" /"c" " + " "1" /"a" " - " "1" /"a" " - " "1" /"b" " - " "1" /"c" ) = "x" ^"0" = 1



Example 8: Simplify: 

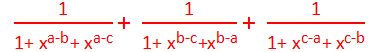
"1" /("1+ " "x" ^"a-b" "+ " "x" ^"a-c" ) "+ " "1" /("1+ " "x" ^"b-c" "+" "x" ^"b-a" ) "+ " "1" /("1+ " "x" ^"c-a" "+ " "x" ^"c-b" )


Solution:

 

Here, 

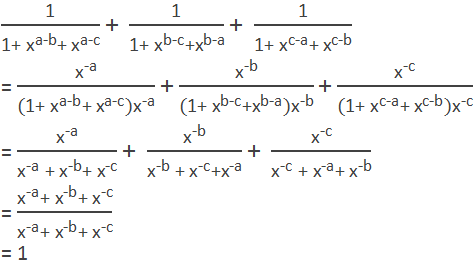
     "1" /("1+ " "x" ^"a-b" "+ " "x" ^"a-c" ) "+ " "1" /("1+ " "x" ^"b-c" "+" "x" ^"b-a" ) "+ " "1" /("1+ " "x" ^"c-a" "+ " "x" ^"c-b" ) = "x" ^"-a" /("(1+ " "x" ^"a-b" "+ " "x" ^"a-c" )"x" ^"-a" ) " + " "x" ^"-b" /("(1+ " "x" ^"b-c" "+" "x" ^"b-a" )"x" ^"-b" ) " + " "x" ^"-c" /("(1+ " "x" ^"c-a" "+ " "x" ^"c-b" )"x" ^"-c" ) = "x" ^"-a" /("x" ^"-a" " + " "x" ^"-b" "+ " "x" ^"-c" ) "+ " "x" ^"-b" /("x" ^"-b" " + " "x" ^"-c" "+" "x" ^"-a" ) "+ " "x" ^"-c" /("x" ^"-c" " + " "x" ^"-a" "+ " "x" ^"-b" ) = ("x" ^"-a" "+ " "x" ^"-b" "+ " "x" ^"-c" )/("x" ^"-a" "+ " "x" ^"-b" "+ " "x" ^"-c" ) = 1

Example 9: Simplify: 

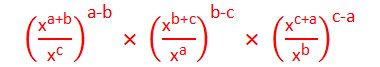
("x" ^"a+b" /"x" ^"c" )^"a-b" " × " ("x" ^"b+c" /"x" ^"a" )^"b-c" " × " ("x" ^"c+a" /"x" ^"b" )^"c-a"


Solution:

 

Here,

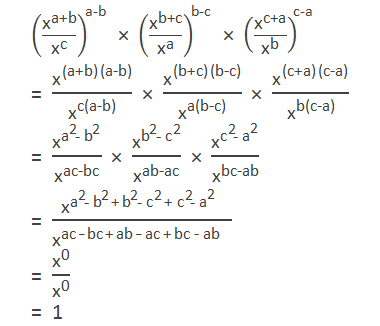
("x" ^"a+b" /"x" ^"c" )^"a-b" " × " ("x" ^"b+c" /"x" ^"a" )^"b-c" " × " ("x" ^"c+a" /"x" ^"b" )^"c-a" = "x" ^("a+b" )"(a-b)" /"x" ^"c(a-b)" " × " "x" ^("b+c" )"(b-c)" /"x" ^"a(b-c)" " × " "x" ^("c+a" )"(c-a)" /"x" ^"b(c-a)" = "x" ^("a" ^"2" "-" "b" ^"2" )/"x" ^"ac-bc" " × " "x" ^("b" ^"2" "-" "c" ^"2" )/"x" ^"ab-ac" " × " "x" ^("c" ^"2" "-" "a" ^"2" )/"x" ^"bc-ab" = "x" ^("a" ^"2" "-" 〖" b" 〗^"2" "+" 〖" b" 〗^"2" "-" 〖" c" 〗^"2" "+" 〖" c" 〗^"2" "-" 〖" a" 〗^"2" )/"x" ^"ac – bc + ab – ac + bc - ab" = "x" ^"0" /"x" ^"0" = "1"
     

 

Example 10: Find the value of: 

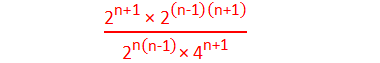
("2" ^"n+1" " × " "2" ^("n-1" )("n+1" ) )/("2" ^"n(n-1)" " × " "4" ^"n+1" )


Solution:

 

Here,

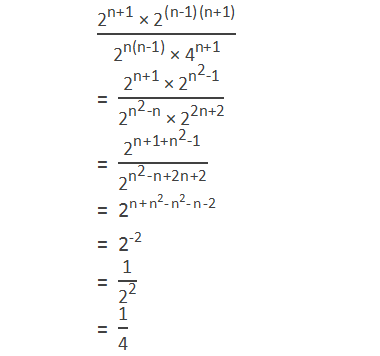
("2" ^"n+1" " × " "2" ^("n-1" )"(n+1)" )/("2" ^"n(n-1)" " × " "4" ^"n+1" ) = ("2" ^"n+1" " × " "2" ^("n" ^"2" "-1" ))/("2" ^("n" ^"2" "-n" ) " × " "2" ^"2n+2" ) = ("2" ^("n+1+" "n" ^"2" "-1" ) " " )/("2" ^("n" ^"2" "-n+2n+2" ) " " ) = "2" ^("n+" "n" ^"2" "-" "n" ^"2" "-n-2" ) = "2" ^"-2" = "1" /"2" ^"2" = "1" /"4"

  

 

If you have any question or problems regarding the law’s  of indices, you can ask here, in the comment section below.


Was this article helpful? LIKE and SHARE with friends…

Labels:

About author: Min Rajbanshi

I am a school math teacher and a blogger since 2012. I do blogging on a variety of topics including math. Over the years, I've explored and written about a wide range of topics, with a particular emphasis on mathematics. My passion for education extends beyond the classroom, as I enjoy sharing knowledge and insights on various subjects through my blog.

4 comments:

  1. UnknownOctober 20, 2021 at 11:37 AM

    X to the power y equal to y to the power x .x equal twice y .

    ReplyDelete
  2. Shona67June 5, 2023 at 12:07 AM

    This comment has been removed by the author.

    ReplyDelete
  3. Keep CalmJune 5, 2023 at 12:17 AM

    Subsequently, to help you in tracking down the best criminal lawyer, examining the different areas and classes of criminal law is fundamental.
    stephenjackcriminallawyer

    ReplyDelete
  4. Alex VolkovAugust 7, 2023 at 6:44 AM

    Corporate mergers and acquisitions are subject to stringent legal scrutiny to ensure fair competition and market efficiency. Yesfinancialfree

    ReplyDelete

Subscribe to: Post Comments (Atom)