Standard Deviation

What is Standard Deviation (SD)?

 

The definition of Standard Deviation: “Standard Deviation is the positive square root of the arithmetic mean of the squares of the deviations of the given observation from their arithmetic mean.”

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Standard deviation is also known as ‘Root Mean-Square Deviation’ because it is the square root of the arithmetic mean of the squares of the deviations.

 

It is denoted by the symbol σ (sigma). 

 

Significance of Standard Deviation

 

Among all the methods of finding dispersion of data, Standard Deviation is regarded as the best. Because, it is free from the defects with which range, quartile deviation and mean deviation suffer. Its value is based upon each and every item of the series and it also takes into account algebraic signs.

 

 

Calculation of Standard Deviation

 

By Direct Method:

 

We calculate the standard deviation for normal data by applying the direct method. In this method, we find directly the arithmetic mean and then deviations from each data.

 

For Individual Series:

The standard deviation of the set of n observations is given by

Where x̄ is the arithmetic mean of the given observations.

 

 

For Discrete or Continuous Series:

 

For a discrete and continuous frequency distribution, the standard deviation is given by

Where x̄ is the arithmetic mean and N is the total number of observations of the given data. In the case of a continuous distribution, x is taken as the mid-value of the corresponding class.

 

 

By Deviation Method:

 

If the values of the observations and their corresponding frequencies are large, then the calculation of standard deviation is tedious and time-consuming. In such cases, we can calculate the standard deviation by taking deviation as follows:

 

 

For Individual Series:

 

When the values of the observations are very large in the individual series, the standard deviation can be calculated by using the following formula,

Where d = x – A  and A is assumed mean.

 

 

For Discrete or Continuous Series:

 

When the values of the observations and the frequencies are large in case of discrete or continuous series, the calculation of standard deviation can be made easy by using the following formula.

Where d = x – A  and A is assumed mean.

 

When the value of variables or mid-values have some common factor, the calculation of the standard deviation can be made still easier by taking the deviation as follows:

Where d = (x – A)/h , A = assumed mean and 'h' is the common factor from all x – A.

 

Coefficient of Standard Deviation

 

The standard deviation is the absolute measure of dispersion. The relative measure of dispersion based on the standard deviation is known as the coefficient of standard deviation. It is given by the formula,

Variance

 

The measure of the dispersion of a random variable or a sample is called Variance. It is given by the square of the standard deviation. So, it is usually denoted by σ² or Var(X) for random variable x.

 

For individual data,

For discrete data,

Coefficient of Variance (C.V.)

 

The Coefficient of Variance (C.V.) is a measure of dispersion equal to the standard deviation of a sample divided by the mean. It is dimensionless and not dependent on the units or scale in which the observations are made. It is often expressed as a percentage.

 

∴ The coefficient of variance (C.V.) is given by the formula,

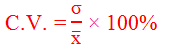
Worked Out Examples

 

Example 1: The weekly expenditure of 5 families in rupees are given below:

Calculate the standard deviation and its coefficient by:

a.     Direct method

b.     Deviation method

 

Solution: Here,

Calculation of Standard Deviation:

 

Direct Method,

Table,

From the Table,

No. of data (N) = 5

∑x = 1775

∑x² = 639375

Deviation method,

Table,

From the Table,

No. of data (N) = 60

∑d = 25

∑d² = 9375

 

Example 2: Find the standard deviation and its coefficient from the following frequency distribution.

Solution: Here,

Calculation of Standard Deviation:

Table,

From the table,

∑fx = 1396

∑fx² = 44396

Example 3: Following are the marks obtained by students in a test exam.

Calculate the standard deviation and it's coefficient by

a.     Direct method

b.     Deviation method

 

Solution: Here,

Calculation of Standard Deviation: 

Direct method

Table,

From the Table,

N = 60

∑fx = 3340

∑fx² = 200300

Deviation method

Table,

From the Table,

N = 60

∑fd = 4

∑fd² = 144

Example 4: Find the variance and its coefficient from the following data.

Solution: Here,

Calculation of Variance:

Table,

From the Table,

∑fx = 1660

∑fx² = 42500

If you have any questions or problems regarding the Standard Deviation, you can ask here, in the comment section below.

 

 

Was this article helpful? LIKE and SHARE with your friends…