Population Growth

 

The population of any country does not remain constant. It generally increases. The relative increase of population over an interval of time is called population growth. Growth per unit time is called growth rate.

 

The way of increasing population is exactly similar to the way of increasing compound amount, because, every year population increases from the previously increased population also.

So, the population of a country or place after T years is given by the formula,

Where,      

P --------> Initial population

P_T -------> Population after T years

R --------> Rate of growth in % per year

T --------> Time in no. of years

 

The growth of the population is also affected by the number of deaths, in-migrants, and out-migrants at the end of the given period of time. In this case,

Where,

D ---------> Number of deaths

M_in -------> In-migrants

M_out ------> Out-migrants

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Some other formulas,

1.     If R₁%, R₂% and R₃% be the rate of population growth of 3 successive years then the population after 3 years is given by:

 

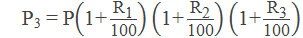
2.     If R₁% be the yearly birth rate, R₂% be the yearly death rate, then the population after T years is given by:

 

 

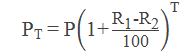
Workout Examples

 

Example 1: The population of a town before 2 years was 75000 and the rate of annual growth of the population of the town is 2%. If the number of in-migrants and out-migrants at the end of 2 years were 880 and 625 respectively and 550 people died within this time interval, find the present population of the town.

 

Solution:

 

Here,

P = 75000

R = 2%

M_in = 880

M_out = 625

D = 550

P_T = ?

 

We have,

 

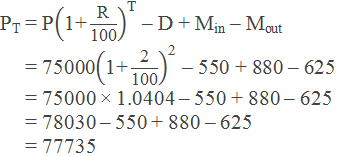
So, the present population of the town is 77735

 

 

Example 2: The present population of a town is 40000. If the yearly birth rate is 5% and death rate is 3%, what will be the population of town after 2 years?

 

Solution:

 

Here,

P = 40000

R₁ = 5%, R₁ = 3%

T = 2 years

P_T = ?

 

We have,

 

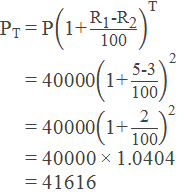
So, the population of the town after 2 years will be 41616.

 

 

Example 3: The population of a village increases every year by 5%. At the end of two years, the total population of the village was 10000. If 1025 were migrated to other places, what was the population of the village in the beginning?

 

Solution:

 

Here,

Total population including the migrated number,

P_T = 10000 + 1025 = 11025

R = 5%

T = 2 years

Present population, P = ?

 

We have,

 

So, the population of the village in the beginning was 10000.

 

 

Example 4: The population of a town before 3 years was 150000. If the annual growth rates of the population in the last 3 years were 2%, 4% and 5% respectively every year, find the population of the town at the end of 3 years.

 

Solution:

 

Here,

P = 150000

R₁ = 2%, R₂ = 4% and R₃ = 5%

T = 3 years

P_T = ?

 

We have,

 

So, the population of the town at the end of 3 years is 167076.

 

 

Example 5: 3years ago, the population of a village was 50000. The population growth rate of village is 2% p.a. 1 year before 420 people died due to an epidemic. Find the present population of the village.

 

Solution:

 

Here,

P = 50000

R = 2%

 

After 2 years (i.e. 1 year before), T = 2 years

 

After 2 years, 420 people died due to epidemic. So,

P = 52020 – 420 = 51600

 

Then, after 1 year (i.e. at present), T = 1 years

 

So, the present population of the village is 52632.

 

 

If you have any questions or problems regarding population growth, you can ask them here, in the comment section below.

 

Was this article helpful? Follow and SHARE with your friends…