
Prime Factors
Prime factors of any whole number are the list
of all prime numbers whose product is equal to that whole number. Each prime
factor can divide the whole number exactly.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
For example, 360 = 2×2×2×3×3×5. Here, {2, 2, 2,
3, 3, 5} is the list of prime factors of 360. Each prime factor 2, 3, and 5 can
divide 360 exactly.
Similarly,
Prime factors of 12 = {2, 2, 3}
Prime factors of 18 = {2, 3, 3}
Prime factors of 20 = {2, 2, 5}
Prime factors of 24 = {2, 2, 2, 3}
Prime factors of 28 = { 2, 2, 7}
Prime factors of 30 = { 2, 3, 5}
Prime factors of 32 = { 2, 2, 2, 2, 2}
Prime factors of 36 = { 2, 2, 3, 3}
Prime factors of 40 = { 2, 2, 2, 5}
Prime factors of 48 = { 2, 2, 2, 2, 3}
Prime factors of 54 = { 2, 3, 3, 3}
Prime factors of 60 = { 2, 2, 3, 5}
Prime factors of 72 = { 2, 2, 2, 3, 3}
Prime factors of 75 = { 3, 5, 5}
Prime factors of 76 = { 2, 2, 19}
Prime factors of 78 = { 2, 3, 13}
Prime factors of 80 = { 2, 2, 2, 2, 5}
Prime factors of 84 = { 2, 2, 3, 7}
Prime factors of 90 = { 2, 3, 3, 5}
Prime factors of 100 = { 2, 2, 5, 5}
Prime factors of 128 = { 2, 2, 2, 2, 2, 2, 2}
Prime factors of 300 = {2, 2, 3, 5, 5}
Prime factors of 600 = {2, 2, 2, 3, 5, 5}
Prime Factorization
The prime factorization is the process of
finding the list of prime factors of a whole number.
For example, 360 = 2×2×2×3×3×5
is the prime factorization of 360.
Similarly,
Prime factorization of 12 = 2×2×3
Prime factorization of 18 = 2×3×3
Prime factorization of 20 = 2×2×5
Prime factorization of 24 = 2×2×2×3
Prime factorization of 28 = 2×2×7
Prime factorization of 30 = 2×3×5
Prime factorization of 32 = 2×2×2×2×2
Prime factorization of 36 = 2×2×3×3
Prime factorization of 40 = 2×2×2×5
Prime factorization of 48 = 2×2×2×2×3
Prime factorization of 54 = 2×3×3×3
Prime factorization of 60 = 2×2×3×5
Prime factorization of 72 = 2×2×2×3×3
Prime factorization of 75 = 3×5×5
Prime factorization of 76 = 2×2×19
Prime factorization of 78 = 2×3×13
Prime factorization of 80 = 2×2×2×2×5
Prime factorization of 84 = 2×2×3×7
Prime factorization of 90 = 2×3×3×5
Prime factorization of 100 = 2×2×5×5
Prime factorization of 128 = 2×2×2×2×2×2×2
Prime factorization of 300 = 2×2×3×5×5
Prime factorization of 600 = 2×2×2×3×5×5
How to find prime factors of a whole number?
We can find the prime factors of any whole number by the following
two methods:
1.
Division method
2.
Factor tree method.
Division Method
In this method, we should go on dividing the given whole number by the least divisible prime number until we get 1 or a prime number as a quotient.
Look at the following worked-out examples of prime factorization by the division method.
Example 1: Factorize 12 by division method.
Solution:
Here, factorizing 12 by division method is as follows:

Solution:
Here, factorizing 18 by division method is as follows:

Example 3: Factorize 32 by division method.
Solution:
Here, factorizing 32 by division method is as follows:

Example 4: Factorize 48 by division method.
Solution:
Here, factorizing 48 by division method is as follows:

Example 5: Factorize 54 by division method.
Solution:
Here, factorizing 54 by division method is as follows:

Solution:
Here, factorizing 72 by division method is as follows:

Example 7: Factorize 100 by division method.
Solution:
Here, factorizing 100 by division method is as follows:
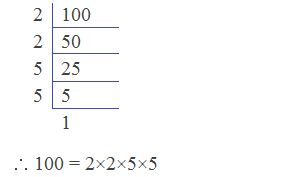
Example 8: Factorize 240 by division method.
Solution:
Here, factorizing 240 by division method is as follows:

Example 9: Factorize 600 by division method.
Solution:
Here, factorizing 600 by division method is as follows:

Example 10: Factorize 1000 by division method.
Solution:
Here, factorizing 1000 by division method is as follows:
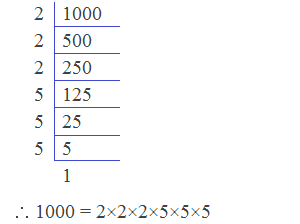
Factor Tree Method
In this method, we should split the whole number into the product of one least prime number and another a composite number. And, again do the same for the composite number. This process goes until we get the product of two prime numbers at last.
Look at the following worked out examples of prime
factorization by the factor tree method.
Example 11: Factorize 12 by factor tree method.
Solution:
Here, factorizing 12 by factor tree method is as follows:

Solution:
Here, factorizing 16 by factor tree method is as follows:

Solution:
Here, factorizing 18 by factor tree method is as follows:
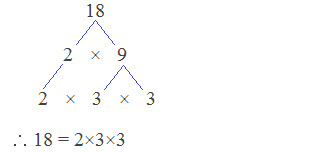
Example 14: Factorize 32 by factor tree method.
Solution:
Here, factorizing 32 by factor tree method is as follows:

Example 15: Factorize 40 by factor tree method.
Solution:
Here, factorizing 40 by factor tree method is as follows:

Example 16: Factorize 54 by factor tree method.
Solution:
Here, factorizing 54 by factor tree method is as follows:

Example 17: Factorize 72 by factor tree method.
Solution:
Here, factorizing 72 by factor tree method is as follows:

Example 18: Factorize 90 by factor tree method.
Solution:
Here, factorizing 90 by factor tree method is as follows:

Example 19: Factorize 120 by factor tree method.
Solution:
Here, factorizing 120 by factor tree method is as follows:

Example 20: Factorize 180 by factor tree method.
Solution:
Here, factorizing 180 by factor tree method is as follows:

If you have any question or problems regarding the Prime Factors, Prime Factorization and Factor Tree, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: