Brackets | BODMAS Rule

Brackets | What are brackets?

 

Brackets are the symbols used to enclose certain variable or numerical expressions that are to be taken together. Brackets are used to change the order in which the operations are to be done. 

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

For example, 7×2+3 = 14+3=17. But, if the sum has to be done at first, then we put brackets within 2+3, i.e. 7×(2+3) = 7×5 = 35.

 

Types of brackets

 

There are 3 types of brackets. They are:

 

( )   Parenthesis or small brackets

{ }   Middle brackets or curly brackets

[ ]   Big brackets or square brackets 

 

Order of use of the brackets

 

When all three types of brackets are in an expression, then we first have to solve within the small brackets( ), then curly brackets{ } and at last the square brackets[ ].

 

 

BODMAS Rule

 

In simplification of integers under the relation of basic operations addition(+), Subtraction(-), multiplication, division(÷) along with the use of brackets, we have to follow the BODMAS Rule.

BODMAS Full Form

 

The full form of BODMAS is, B for Brackets, O for Of, D for Division, M for Multiplication, A for Addition and S for Subtraction.

 

 

Meaning of BODMAS Rule

 

According to BODMAS rule, first we have to follow the Brackets, second Of, third Division, fourth Multiplication, fifth Addition, and sixth Subtraction.

 

There may be sometimes a Vinculum inside the brackets. Vinculum is an overline for certain numbers. And, we have to solve the numbers under the vinculum at first.

 

Here is the table for order of operation according to the BODMAS rule.

Here are some BODMAS Questions with Answers:

 

Worked Out Examples

 

Example 1: Simplify: 7 + 8 – 9 ÷ 3 × 2

 

Solution: Here,

   

7 + 8 – 9 ÷ 3 × 2

= 7 + 8 – 3 × 2

= 7 + 8 – 6

= 15 – 6

= 9 Ans.

 

 

Example 2: Simplify: 54 ÷ [{16 – (3 – 2)} – 6]

 

Solution: Here,

   

54 ÷ [{16 – (3 – 2)} – 6]

= 54 ÷ [{16 – 1} – 6]

= 54 ÷ [15 – 6]

= 54 ÷ 9

= 6 Ans.

 

 

Example 3: Simplify: 52 – 4 of (17 – 12) + 4 × 7

 

Solution: Here,

   

52 – 4 of (17 – 12) + 4 × 7

= 52 – 4 of 5 + 4 × 7

= 52 – 20 + 4 × 7

= 52 – 20 + 28

= 80 – 20

= 60 Ans.

Example 4: Simplify:

Solution: Here, 

Example 5: Simplify:

Solution: Here,

 

Example 6: Simplify: 13 × 5 ÷ [{12 ÷ (4 – 2)} – 2]

 

Solution: Here,

 

13 × 5 ÷ [{12 ÷ (4 – 2)} – 1]

= 13 × 5 ÷ [{12 ÷ 2} – 1]

= 13 × 5 ÷ [6 – 1]

= 13 × 5 ÷ 5

= 13 × 1

= 13 Ans.

 

 

Example 7: Simplify: 8 × 3 + [63 ÷ {18 ÷ 3 (9 – 17 + 5 × 2)}]

 

Solution: Here,

 

8 × 3 + [63 ÷ {18 ÷ 3 (9 – 17 + 5 × 2)}]

= 8 × 3 + [63 ÷ {18 ÷ 3 (9 – 17 + 10)}]

= 8 × 3 + [63 ÷ {18 ÷ 3 of 2}]

= 8 × 3 + [63 ÷ {18 ÷ 6}]

= 8 × 3 + [63 ÷ 3]

= 8 × 3 + 21

= 24 + 21

= 45 Ans.

 

 

BODMAS in Fractions:

 

Example 8: Simplify:

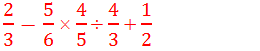
Solution: Here,

Example 9: Simplify:

Solution: Here,

 

Example 10: Simplify:

Solution: Here,

If you have any questions or problems regarding the Brackets and BODMAS Rule, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…