
Cardinality of Sets
Let, A be a finite set. The number of elements in set A is called the cardinal number of set A. It is denoted by n(A). If A = {a, b, c, d, e}, the number of elements in set A is 5, therefore the cardinal number of set A, i.e. n(A) = 5.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Let, U be the universal set, A and B be any two finite and overlapping subsets of U. Then,
n(U) = Number of elements in
set U
n(A) = Number of elements in
set A
n(B) = Number of elements in
set B
n(A∪B) = Number of elements in set A∪B
n(A∩B) = Number of elements in
A∩B
no(A) = Number of elements
in set A only
no(B) = Number of elements
in set B only
n(A∪B)c = Number of elements in
set (A∪B)c
The properties based on the cardinal number of sets are called the cardinality of sets.
Method for finding
cardinality of sets
Look at the following Venn-diagrams,

In above venn-diagram, sets A and B are disjoint sets with n(A) = 4 and n(B) = 3. Both the sets A and B doesn’t have any common elements. So, n(A∩B) = 0 and n(A∪B) = 4 + 3 = 7.
Therefore, for disjoint sets A and B,
n(A∪B) = n(A) + n(B)
n(A∩B) = 0

In above venn-diagram, sets A and B are intersecting or overlapping sets with n(A) = 5 and b(B) = 4. Sets A and B have 2 elements common. So, n(A∩B) = 2. There are altogether 7 elements within A and B. So, n(A∪B) = 7. Which can be obtained by applying the formula,
n(A∪B) = n(A) + b(B) – n(A∩B)
= 5 + 4 – 2
= 7
The total elements within the universal set U is 10. So, n(U) =
10. Outside of A and B, there are 3 elements. So, n(A∪B)c = 3. So, we can have the following additional
formula,
n(A∪B) = n(U) – n(A∪B)c
n(A∪B)c = n(U) –
n(A∪B)
n(U) = n(A∪B) + n(A∪B)c
There are 3 elements in A – B or A only part, so no(A)
= 3. Similarly no(B) = 2. So, we have the following results as well,
no(A) = n(A) – n(A∩B)
no(B) = n(B) – n(A∩B)
n(A∪B) = no(A) + no(B)
+ n(A∩B)
n(U) = no(A) + no(B) + n(A∩B) + n(A∪B)c
Therefore, for overlapping sets A and B,
n(A∪B) = n(A) + b(B) – n(A∩B)
n(A∪B) = n(U) – n(A∪B)c
So, we have the
following list of cardinality formula of sets:
If A and B are subsets of universal set U then,
1.
n(A∪B) = n(A) + n(B) – n(A∩B)
2.
n(A∩B) = n(A) + n(B)
- n(A∪B)
3.
n(A∪B)c = n(U) – n(A∪B)
4.
no(A) =
n(A) – n(A∩B)
5.
no(B) =
n(B) – n(A∩B)
6.
n(A∪B) = no(A) + no(B) + n(A∩B)
7.
n(U) = no(A)
+ no(B) + n(A∩B) + n(A∪B)c
8.
n(U) = n(A) + n(B) +
n(A∪B)c – n(A∩B)
Some languages and their set-notations used in the problems on cardinality of sets:
1.
Both = n(A∩B)
2.
At least one = n(A∪B)
3.
Exactly one = no(A)
+ no(B)
4.
None of them = n(A∪B)c
Word Problems based
on Sets and Venn Diagrams
Worked Out Examples
Example 1: In the given venn-diagram A and B are two subsets of an universal set where n(U) = 50, n(A) = 23, n(B) = 20 and n(A∩B) = 8.

Find the following:
a.
n(A∪B)
b.
n(A∪B)c
c.
no(A)
d.
no(B)
e.
Exactly one =?
Solution:
Here,
n(U) = 50
n(A) = 23
n(B) = 20
n(A∩B) = 8
a. n(A∪B) = n(A) + n(B) – n(A∩B)
= 23 + 20 – 8
= 35
b.
n(A∪B)c = n(U) – n(A∪B)
= 50 – 35
= 15
c.
no(A) =
n(A) – n(A∩B)
= 23 – 8
= 15
d. no(B) = n(B) – n(A∩B)
= 20 – 8
= 12
e.
Exactly one = no(A)
+ no(B)
= 15 + 12
= 27
Example 2: Out of 50 students of class IX, 25 students liked to play football,
35 liked to play basketball and 15 liked to play both the games. How many
students do not like to play any games? Show the above information in a
Venn-diagram.
Solution:
Let the set of students
who like football and basketball be F and B.
n(U) = 50
n(F) = 25
n(B) = 35
n(F∩B) =
15
n(F∪B)c = ?
We Know,
n(F∪B) = n(F) + n(B) – n(F∩B)
= 25 + 35 – 15
= 45
Now,
n(F∪B)c = n(U) – n(F∪B)
= 50 – 45
= 5
Venn-diagram,

∴ 5 students do not like to play any games. Ans.
Example 3: In a class of 30 students, 20 students like to play cricket and 15
like to play volleyball. Also, each student like to play at least one of the
two games. How many students like to play both games? Illustrate the above
information in a Venn-diagram.
Solution:
Let, the set of students who like to play cricket and volleyball
be C and V.
n(U) = 30
n(C) = 20
n(V) = 15
Each student like to play at least one game. Therefore,
n(C∪V) = n(U) = 30
Now,
n(C∩V) = n(C) + n(V) – n(C∪V)
= 20 + 15 – 30
= 5
Venn-diagram,

∴ 5 students like to play both games. Ans.
Example 4: In a survey of a community, it was found that 85% of people like the winter season and 65% like the summer season. If none of them did not like both
seasons,
a.
Present the above information
in a Venn-diagram.
b.
What percent liked both
the seasons?
c.
What percent liked winter
season only?
Solution:
Let, the set of people who liked winter and summer be W and S.
n(U) = 100%
n(W) = 85%
n(S) = 65%
Since none of them did not like both the seasons,
n(W∪S) = n(U) = 100%
Now,
n(W∩S) = n(W) + n(S) – n(W∪S)
= 85 + 65 –
100%
= 50%
a. Venn-diagram,

b.
n(W∩S) = 50% like
both the seasons.
c.
no(W) =
n(W) – n(W∩S)
= 85 – 50%
= 35% like winter season only.
Example 5: In a group of 100 people, 72 can speak English and 43 can speak
Hindi. How many can speak English only? How many can speak Hindi only and how
many can speak both Hindi and English?
Solution:
Let the set of students who can speak English and Hindi be E and
H.
n(U) = 100
n(E) = 72
n(H) = 43
Since, each person can speak at least one language,
n(E∪H) = n(U) = 100
Now,
n(E∩H) = n(E) + n(H) – n(E∪H)
= 72 + 43 – 100
= 15
Now,
no(E) = n(E) – n(E∩H) = 72 – 15 = 57
no(H) = n(H) – n(E∩H) = 43 – 15 = 28
Therefore,
no(E) = 57 people can speak English only.
no(H) = 28 people can speak Hindi only.
n(E∩H) = 15 people can speak both the languages.
Example 6: Out of 100 students, 80 passed science, 71 mathematics, 10
failed both subjects and 7 did not appear in the examination. Find the number
of students who passed both subjects by representing the above information
in a Venn-diagram.
Solution:
Let the set of students
who passed science and mathematics be S and M.
n(U) =
100
n(S) = 80
n(M) = 71
n(S∪M)c = 10 + 7 = 17
n(S∩M) =
?
We Know,
n(S∪M) = n(U) – n(S∪M)c
= 100 – 17
= 83
Now,
n(S∩M) =
n(S) + n(M) – n(S∪M)
= 80 + 71 – 83
= 68
Venn-diagram,
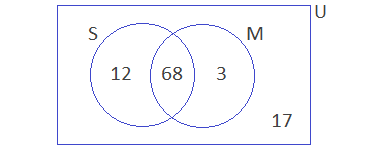
Hence 68 students passed both the subjects.
Example 7: In a survey of 100 farmers, the ratio of the farmers who grew paddy
and wheat is 2:3. If 10 farmers grew both and 20 grew none of them, find the
numbers of farmers who grew paddy only by using Venn-diagram.
Solution:
Let, the set of farmers who grew paddy and wheat be P and W.
n(U) = 100
n(P) = 2x, and n(W) = 3x (let)
n(P∩W) = 10
n(P∪W)c = 20
We know,
n(P∪W) = n(U) – n(P∪W)c
= 100 – 20
= 80
i.e. n(P) + n(W) –
n(P∩W) = 80
or, 2x + 3x – 10 = 80
or, 5x = 80 + 10
or, 5x = 90
or, x = 90/5
or, x = 18
Therefore,
n(P) = 2x = 2 × 18 = 36
n(W) = 3x = 3 × 18 = 54
And,
no(P) = n(P) – n(P∩W)
= 36 – 10
= 26 Ans.
Venn-diagram,

∴ 26 people grew paddy only.
Example 8: In a group of total students 35 enrolled in art class and 57
enrolled in dance class. Find the number of students who are either in art
class or in dance class, if the situation is:
a.
When two classes meet at
the same hour.
b.
When two classes meet at a different hour and 12 students are enrolled in both activities.
Solution:
Let, the set of students enrolled in art and dance class be A
and D.
n(A) = 35
n(D) = 57
a.
When two classes meet at the same hours then n(A∩D) = 0.
n(A∪D) = n(A) + n(D) – n(A∩)
= 35 + 57 – 0
= 92
∴ 92 students are either in art or in dance class.
b.
When two classes meet at different hours then n(A∩D) = 12.
n(A∪D) = n(A) + n(D) – n(A∩)
= 35 + 57 – 12
= 80
∴ 80 students are either in art or in dance class.
Example 9: In a survey, it was found that 80% of people liked oranges, 85% liked
mangoes and 75% liked both. But 45 people liked none of them. By drawing a Venn
diagram, find the number of people who were in the survey.
Solution:
Let the set of students
who like orange and mango be O and M.
n(U) =
100%
n(O) = 80%
n(M) = 85%
n(O∩M) =
75%
n(O∪M)c = 45
We Know,
n(O∪M) = n(O) + n(M) – n(O∩M)
= 80% + 85% – 75%
= 90%
Now,
n(O∪M)c = n(U) – n(O∪M)
= 100% – 90%
= 10%
Let, the
total number of people in the survey be ‘x’.
∴ 10% of x = 45
or, 10/100 × x = 45
or, 1/10 × x = 45
or, x = 450
Venn-diagram,

Hence,
the number of people who were in the survey is 450.
Example 10: In an election, there were 400 voters, A and B were two candidates.
The ratio of votes of A and B is 4:3. If 40 voters cast votes for both and 10
voters didn’t cast the vote, find
a.
No. of votes got by A.
b.
Total no of valid votes.
Solution:
Here,
n(U) = 400
The ratio of 4:3 is only for the valid votes, therefore
no(A) = 4x and no(B) = 3x (let)
n(A∩B) = 40 (invalid votes)
n(A∪B) = 10
We know,
no(A) + no(B) + n(A∩B) + n(A∪B)c = n(U)
i.e. 4x + 3x + 40 + 10
= 400
or, 7x + 50 = 400
or, 7x = 400 – 50
or, 7x = 350
or, x = 350/7
or, x = 50
Therefore,
a.
No of votes got by A
= no(A) = 4x = 4 × 50 = 200
b.
Total no. of valid
votes = no(A) + no(B) = 4x + 3x = 7x = 7 × 50 = 350
If you have any questions or problems regarding the Cardinality of Sets, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



A survey shows that 63% of Americans like cheese whereas 76% like apples. What can you say about the % of Americans who like both cheese and apple.
ReplyDeleteSolution: Here,
DeleteLet the set of Americans who like cheese and apple be C and A respectively.
n(U) = n(C∪A) = 100%
n(C) = 63%
n(A) = 76%
n(C∩A) = ?
We know,
n(C∩A) = n(C) + n(A) – n(C∪A)
= 63 + 76 – 100%
= 39%
∴ 36% of Americans like both cheese and apple.