Isosceles Triangle
A triangle with any two sides equal is called an isosceles
triangle. The unequal side is known as the base, and the two angles at the ends
of base are called base angles. And, the angle opposite to base is called the
vertical angle.
In the given figure of triangle ABC, AB = AC, so it is an
isosceles triangle. BC is the base, ∠ABC and ∠ACB are base angles and ∠BAC is the vertical
angle.
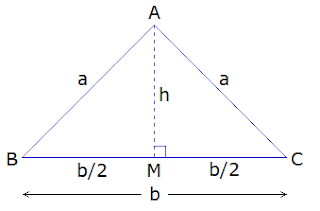 Let ΔABC be an
isosceles triangle. AB = AC = a, and the base BC = b. Then AM⊥BC is drawn. Thus, AM = h and BM = CM = b/2
Let ΔABC be an
isosceles triangle. AB = AC = a, and the base BC = b. Then AM⊥BC is drawn. Thus, AM = h and BM = CM = b/2
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Area of an isosceles triangle
 Let ΔABC be an
isosceles triangle. AB = AC = a, and the base BC = b. Then AM⊥BC is drawn. Thus, AM = h and BM = CM = b/2
Let ΔABC be an
isosceles triangle. AB = AC = a, and the base BC = b. Then AM⊥BC is drawn. Thus, AM = h and BM = CM = b/2Properties (theorems) of isosceles triangle:
1. Base angles of an isosceles triangle are
equal.
2. The bisector of vertical angle of an
isosceles triangle is perpendicular to the base.
3. The bisector of the vertical angle of an
isosceles triangle bisects the base line segment.
Theoretical proofs:
Theorem 1. “Base angles of an isosceles triangle are equal.”
Given: In triangle ABC,
AB = AC
To prove: ∠B = ∠C
Construction: AM⊥BC drawn.
Proof:
Statements Reasons
1. In
ΔABM and ΔACM
i. ∠AMB = ∠AMC (R) -----> both being right angles (AM⊥BC).
ii. AB = AC (H) ---------------> given.
iii. AM = AM (S) --------------> being common side.
2. ΔABM ≅ ΔACM --------------> by R.H.S. axiom.
3. ∠ABM = ∠ACM ------------>
corresponding angles of ≅ triangles.
4. ∠B = ∠C
------------------------> from statement 3.
Proved.
Note: The converse of theorem-1
is also true i.e. if two angles of a triangle are equal, then the sides
opposite to them are equal.
Theorem 2. “The bisector of vertical angle of isosceles triangle is
perpendicular to the base.”
Given: In ΔABC, AB = AC
and AD is the bisector of vertical angle ∠BAC i.e. ∠BAD = ∠CAD.
To
prove: AD⊥BC
Proof:
Statements Reasons
1. In ΔABD and ΔACD
i. AB = AC (S) -------------> given.
ii. ∠BAD = ∠CAD (A) -----------> given.
iii. AD = AD (S) ---------------> common side.
2. ΔABD ≅ ΔACD --------------> by S.A.S. axiom.
3. ∠ADB = ∠ADC ----------> corresponding angles of ≅ triangles.
4. AD⊥BC
---------> being linear pair angles equal (statement 3.)
Proved.
Note: The converse of theorem-2
is also true i.e. if the line segment from vertex is perpendicular base then it
bisects the vertical angle.
Theorem
3. “The bisector of the vertical angle of an isosceles triangle bisects the base line segment.”
Given: In ΔABC, AB = AC
and AD is the bisector of vertical angle ∠BAC i.e. ∠BAD = ∠CAD.
To
prove: BD = DC
Proof:
Statements Reasons
1. In ΔABD and ΔACD
i. AB = AC (S) ----------------> given.
ii. ∠BAD = ∠CAD (A) -----------> given.
iii. AD = AD (S) ---------------> common side.
2. ΔABD ≅ ΔACD -------------> by S.A.S. axiom.
3. BD = DC -----------> corresponding sides of ≅ triangles.
Proved.
Note: The converse of theorem-3
is also true i.e. the line joining the vertex to mid-point of the base bisects
the vertical angle.
Workout Examples
Example 1: Find the angles indicated by x and y
in the given figure.
Solution:
From the figure,
x
= 60° --------> base angles of isosceles Δ.
y
+ 60° = 90° --------> exterior angle of a Δ is equal to the sum of two
opposite interior angles.
or, y = 90° – 60°
or, y = 30°
∴
x = 60° and y = 30°
Example 2: Find the angles indicated by x and y
in the given figure.
Solution:
From the figure,
∠HTM = x ---------> being HT = HM
∠BHT = y -----------> being HT = BT
∠HTM = ∠HBT + ∠BHT ------> exterior angle of a Δ is equal to the sum of
two opposite interior angles.
or, x = y + y
or, x = 2y ----------------(i)
x
+ y = 90° ------> exterior angle of a Δ is equal to the sum of two
opposite interior angles.
or, 2y + y = 90° -----------> putting x
= 2y from (i)
or, 3y = 90°
or, y = 90°/3
or, y = 30°
x
= 2y
= 2 × 30°
= 60°
∴
x = 60° and y = 30°
Example 3: Find the a, b, c, d and e from the
given figure.
Solution:
From the figure,
a
= 37° --------> base angles of isosceles Δ.
a
+ b + 37° = 180° --------> sum of angles of a Δ.
or, 37° + b + 37° = 180°
or, b + 74° = 180°
or, b = 180° – 74°
or, b = 106°
c
+ b = 180° ---------> linear pair of angles.
or, c + 106° = 180°
or, c = 180° – 106°
or, c = 74°
d
= c -----------> base angles of isosceles Δ.
= 74°
74°
+ 74° + e = 180° ------> sum of angles of a Δ.
or, 148° + e = 180°
or, e = 180° – 148°
or, e = 32°
∴
a = 37°, b = 106°, c = 74°, d = 74° and e = 32°
You can comment
your questions or problems regarding isosceles triangle here.












0 comments: