Corresponding Angles
When two lines are cut by a transversal, then a pair of non-adjacent angles on the same side of a transversal, one external and the other internal are called corresponding angles.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
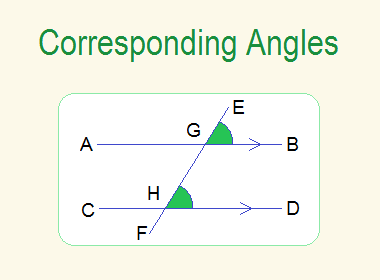
In the figure given below, transversal EF has been cut to the two non-parallel lines AB and CD at G and H.

Here, the corresponding angles are:
i.
∠AGE and ∠GHD
ii.
∠AGH and ∠DHF
iii.
∠EGB and ∠GHC
iv. ∠BGH and ∠CHF
If two parallel lines are cut by a transversal then the corresponding angles are equal. In below figure, transversal RS has been cut to the two parallel lines MN and PQ at A and B.

So, the
corresponding angles are equal. i.e.
i.
∠RAM = ∠ABP
ii.
∠MAB = ∠PBS
iii.
∠RAN = ∠ABQ
iv.
∠NAB = ∠QBS
Worked Out Examples
Example 1: Find the value of x from the given figure.

Solution:
Here,
From the figure,
5x – 3° = 3x + 17°
------> Corresponding angles.
or, 5x – 3x = 17° + 3°
or, 2x = 20°
or, x = 20°/2
or, x = 10° Ans.
Example 2: Find the value of a and b from the given figure.

Solution:
Here,
From the figure,
a = 70° ------>
Corresponding angles.
b = a ------>
Corresponding angles.
= 70°
∴ a = 70° and b = 70° Ans.
Example 3: Find the value of a, b and c from the given figure.

Solution:
Here,
From the figure,
a = 50° ------>
Corresponding angles.
b = 70° ------>
Corresponding angles.
Now,
c + 50° + 70° = 180°
------> Sum of angles of a Δ.
or, c + 120° = 180°
or, c = 180° – 120°
or, c = 60°
∴ a = 50°, b = 70° and c = 60° Ans.
If you have any questions or problems regarding the Corresponding Angles, you can ask here, in the comment section below.
Was this article helpful? LIKE and SHARE with your friends…



0 comments: