How to Solve Equations by Elimination Method?

Among the various methods to solve simultaneous equations, the Elimination Method is one of the most popular and easiest methods to solve the pair of simultaneous equations in two variables x and y.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

In this method, one variable either x or y is eliminated to find the value of another variable. And, for that, we need to make coefficients of any one variable equal by multiplying or dividing the equations by the least number so that the coefficients of x or y become equal in both the new equations. 

Then, by adding or subtracting according to these equal coefficients have opposite or same sign respectively, we get an equation which will have only one variable. Then, simplification will give the value of that variable.

 

After solving the value of either x or y obtained from the above steps is substituted in any one of the given equations to get the value of the other variable.

Steps for solving simultaneous equations by elimination method:

 

Step 1: Convert one variable of both equations with the same coefficient.

Step 2: Eliminate the variable having the same coefficient by subtracting or adding.

Step 3: Solve the equation having one variable.

Step 4: Substitute the value of one variable so obtained in any one of the given equations to calculate the value of another variable.

 

This process of Elimination Method will be clear by the following worked out examples.

 

 

Worked Out Examples

 

Example 1: Solve: x + 3y = 13 and x + y = 7 by elimination method.

Solution: Here,

x + 3y = 13 …………. (i)

x + y = 7 ………….. (ii)

Subtracting equation (ii) from (i), we get,

Now, substituting the value of y = 3 in equation (ii), we get,

        x + 3 = 7

or,    x = 7 – 3

or,    x = 4

Hence, x = 4 and y = 3.

Example 2: Solve: x + 2y = 5 and 5x – 2y = 13 by elimination method.

Solution: Here,

x + 2y = 5 …………. (i)

5x – 2y = 13 ………….. (ii)

Adding equations (i) and (ii) we get,

Now, substituting the value of x = 3 in equation (i) we get,

        3 +2y = 5

or,    2y = 5 – 3

or,    2y = 2

or,    y = 1

Hence, x = 3 and y = 1.

Example 3: Solve: 3x + 5y = 7 and 7x + 10y = 13 by elimination method.

Solution: Here,

        3x + 5y = 7 …………. (i) × 2

        7x + 10y = 13 ………….. (ii)

Multiplying equation (i) by 2 and subtracting from equation (ii) we get,

Now, substituting the value of x = –1 in equation (i) we get,

        3 × –1 + 5y = 7

or,    –3 + 5y = 7

or,    5y = 7 + 3

or,    5y = 10

or,    y = 2

Hence, x = –1 and y = 2.

Example 4: Solve: 5x + 3y = 5 and 3x – 4y = 32 by elimination method.

Solution: Here,

        5x + 3y = 5 …………. (i) × 4

        3x – 4y = 32 ………….. (ii) × 3

Multiplying equation (i) by 4 and (ii) by 3 and then adding we get,

Now, putting x = 4 in equation (i) we get,

        5 × 4 + 3y = 5

or,    20 + 3y = 5

or,    3y = 5 – 20

or,    3y = –15

or,    y = –5

Hence, x = 4 and y = –5.

 

 

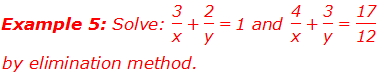
Solution: Here,

Multiplying equation (i) by 3 and (ii) by 2 and subtracting (ii) from (i), we get,

Now, substituting the value of x = 6 in equation (i), we get,

        3/6 + 2/y = 1

or,    1/2 + 2/y = 1

or,    2/y = 1– 1/2

or,    2/y = 1/2

or,    y = 4

Hence, x = 6 and y = 4.

Do you have any questions regarding the elimination method?

You can ask your questions or problems here in the comment section below.