Distance Formula | Distance Between Two Points

 

We can find the distance between two points when the co-ordinates of the two points are given. We calculate that distance by using a formula called distance formula which is derived as follows.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Let P(x₁, y₁) and Q(x₂, y₂) be two given points in the coordinate plane. Draw perpendicular PL from P to the x-axis. Then, OL = x₁ and PL = y₁. Draw perpendicular QM from Q to the x-axis. Then, OM = x₂ and QM = y₂.

Again, draw perpendicular PN from P to the line segment QM. Then,

PN = LM = OM – OL = x₂ – x₂

QN = QM – NM = QM – PL = y₂ – y₁

From right-angled DPNQ, by Pythagoras theorem,

PQ² = PN² + QN²

       = (x₂ – x₁)² + (y₂ – y₁)²

This is the distance formula between two points P(x₁, y₁) and Q(x₂, y₂). An only positive square root is to be taken because PQ being the distance between two points is positive.

 

Distance from origin

 

The distance of the point (x, y) from the origin (0, 0),

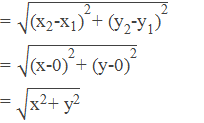
Remarks:

1.     The formula remains the same if the points P(x₁, y₁) and Q(x₂, y₂) are taken in different quadrants.

2.     If a point lies on x-axis, its ordinate is zero. Therefore, any point on x-axis can be taken as (x, 0).

3.     If a point lies on y-axis, its abscissa is zero. Therefore, any point on y-axis can be taken as (0, y).

4.     To prove that a quadrilateral is a,

        (i)        rhombus, show that all sides are equal.

        (ii)     square, show that all sides are equal and diagonals are also equal.

        (iii)  parallelogram, show that the opposite sides are equal.

        (iv)   rectangle, show that the opposite sides are equal and diagonals are also equal.

5.     To prove that a triangle is a,

        (i)      scalene, show that none of the sides are equal.

        (ii)   isosceles, show that two sides are equal.

        (iii) equilateral, show that all sides are equal.

        (iv)  right angled triangle, show that square of one side is equal to the sum of the squares of other two sides.

 

 

Application of Distance Formula

 

We can apply the distance formula to find the distance between any two points on the coordinate plane. And this can be applied for various geometrical and mathematical purposes such as to find the coordinates of any point under the given conditions, to find the center of circum-circle, to verify a square, rectangle, or parallelogram, etc. Look at the following examples:

 

 

Workout Examples

 

Example 1: Find the distance between the points A(-8, 2) and B(4, 7).

Solution: Here,

A(-8, 2)

B(4, 7)

∴  x₁ = -8    x₂ = 4

    y₁ = 2      y₂ = 7

By using distance formula,

 

Example 2: If the distance between two points (-3, 4) and (a, 1) is 5 units, find the possible values of a.

Solution: Here,

Given points are (-3, 4) and (a, 1)

Distance = 5 units

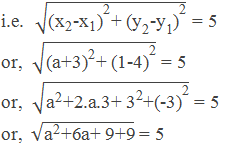
or,  a² + 6a + 18 = 5² [squaring]

or,  a² + 6a + 18 = 25

or,  a² + 6a + 18 – 25 = 0

or,  a² + 6a – 7 = 0

or,  a² + (7 – 1)a – 7 = 0

or,  a² + 7a – a – 7 = 0

or,  a(a + 7) – 1(a + 7) = 0

or, (a + 7)(a – 1) = 0

Either, a + 7 = 0

           or,  a = -7

∴  Or,  a – 1 = 0

           or,  a = 1

∴  a = 1 or -7

 

Example 3: Find the centre and radius of the circum-circle of a trianle having vertices (-4, 1), (-2, 5) and (1, -4).

Solution: Here,

A(-4, 1), B(-2, 5) and C(1 -4)

Let, P(x, y) be the centre of the circum-circle,

∴ PA = PB = PC

Taking PA = PB,

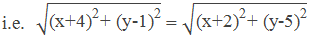
or,  x² +2.x.4+4²+y²-2.y.1+1² = x²+2.x.2+2²+y²-2.y.5+5²

or,  x² +8x+16+y²-2y+1 = x²+4x+4+y²-10y+25

or,  8x–2y-4x+10y = 4+25-16-1

or,  4x+8y = 12

or,  4(x+2y) = 12

or,  x+2y = 3 ------------> (i)

Again, taking PB = PC,

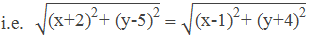
or,  x²+2.x.2+2²+y²-2.y.5+5² = x²-2.x.1+1²+y²+2.y.4+4²

or,  x²+4x+4+y²-10y+25 = x²-2x+1+y²+8y+16

or,  4x–10y+2x-8y = 1+16-4-25

or,  6x-18y = -12

or,  6(x-3y) = -12

or,  x-3y = -2 ------------> (ii)

Subtracting equation (ii) from equation (i), we get,

Putting y = 1 in equatin (i), we get,

          x + 2×1 = 3

or,     x + 2 = 3

or,     x = 3 – 2

or,     x = 1

∴  Centre of circle is P(1, 1), and

 

Example 4: Prove that the points (1, 3), (2, 5), (6, 3), and (5, 1) are the vertices of a rectangle.

Solution: Let,

P(1, 3), Q(2, 5), R(6, 3) and S(5, 1)

∴ 

Since, PQ = RS, QR = PS and diagonals PR = QS, PQRS is a rectangle.

 

If you have any questions or problems regarding the Distance Formula, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…