
What is a linear equation?
The definition of linear equation is: “The
first degree equations in one, two, or three variables are called Linear Equations.”
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
So, the equations of the form: ax + b = 0, ax + by + c = 0 and
ax + by + cz + d = 0 are linear equations in one, two and three variables x, y
and z where a, b, c and d are real numbers and not equal to zero at a time.
x = 1, 2x + 3 = 0, x + 4y = 7, 5x – 2y = 3, x + 3y – 4z = 1 etc.
are some examples of linear equations.
What does a Linear equation do?
In coordinate geometry,
-
Linear equations in one variable
represents the straight lines parallel to the axes on a coordinate plane.
-
Linear equations in two
variables represent the oblique straight lines on a coordinate plane.
-
Linear equations in three
variables always represent a plane on a three-dimensional space.
Linear Equations in two Variables
Linear equation in
two variables x and y is an equation of
the form ax + by + c = 0, where a, b and c are real numbers and both a and b
are not equal to 0 at a time.
2x + 3y = 6 and x + 4y = 7 are some examples of linear equation
in two variables. These equation can also written in the form 2x + 3y – 6 =
0, x + 4y – 7 = 0 respectively.
Note: Equations of the type ax+b=0 are also examples of linear
equations in two variables because they can be expressed as ax+0.y+b=0. For
example, 4-3x=0 can be written as -3x+0.y+4=0
Solving Linear Equations
Solving linear a
equation ax + by + c = 0 is to find the points
(x, y) or pair of values of x and y which satisfy the given linear equation.
For example the point (2, 3) is the solution of the linear equation 2x + 3y –
13 = 0. Because for the value of x = 2 and y = 3 satisfy the equation 2x + 3y –
13 = 0,
i.e 2x2 + 3x3 – 13 = 0
or, 4 + 9 – 13 = 0
or, 13 – 13 = 0
or, 0 = 0 (True)
How to Solve Linear Equation?
To solve a linear equation in two variables x and y, we express
the value of any one variable in terms of another variable. And then, by
choosing some values for the second variable, we can find the corresponding
values of the first variable.
For example, look at the following solutions of linear
equations.
Example 1: Find the solutions of the linear equation y – 3x = 4.
Solution: Here,
Finding the value of y in terms of x,
y – 3x = 4
or, y = 4 + 3x
Now, by choosing some values of x we can find the corresponding values of y as given in the table below.
Table,
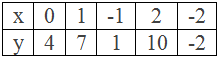
∴ The the solutions of linear equation y – 3x =
4 are: (0, 4), (1, 7), (-1, 1), (2, 10) and (-2, -2)
Example 2: Find the solutions of the linear equation 3x + 4y = 10.
Solution: Here,
Finding the value of x in terms of y,
3x + 4y = 10
or, 3x = 10 – 4y
or, x = (10 – 4y)/3
Now, by choosing some values of y we can find the corresponding values of x as given in the table below.
Table,
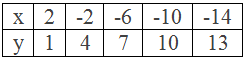
∴ The the solutions of the linear equation 3x +
4y = 10 are: (2, 1), (-2, 4), (-6, 7), (-10, 10) and (-14, 13)
Note: A linear equation in two variables has infinitely many
solutions.
Graphing Linear Equations
By plotting the solution points of a linear equation on a
coordinate plane and joining them, we will get a straight line on the graph,
which is called the Graph of Linear Equation.
Some of the special cases:
1.
x=0 is the equation of
y-axis and y=0 is the equation of the x-axis.
2.
The graph of x=a is a
straight line parallel to the y-axis.
3.
The graph of y=b is a
straight line parallel to the x-axis.
4.
The graph of the equation in the form y=mx is a line that always passes through the origin.
For example, look at the following solutions of linear equations
and their graphs.
Example 3: Draw the graph of x + y = 7.
Solution: Here,
x + y = 7
or, x = 7 – y
Table,
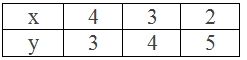
∴ Three solutions of the given linear equation x + y = 7 are (4, 3),
(3, 4) and (2, 5).
Now, plotting these points on a graph, and joining them by a straight line we get following graph of linear equation.

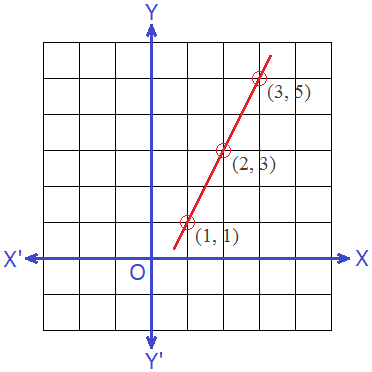
Example 4: Draw the graph of 2x – y = 1.
Solution: Here,
2x – y =1
or, 2x = 1 + y
or, x = (1 + y)/2
Table,
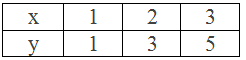
∴ Three solutions of the given linear equation 2x – y = 1 are (1,
1), (2, 3) and (3, 5).
Now, plotting these points on a graph, and joining them by a straight line we get following graph of linear equation.
Example 5: Draw the graph of 2x + 3y = 6.
Solution: Here,
2x + 3y = 6
or, 2x = 6 – 3y
or, x = (6 – 3y)/2
Table,
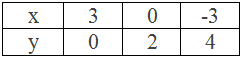
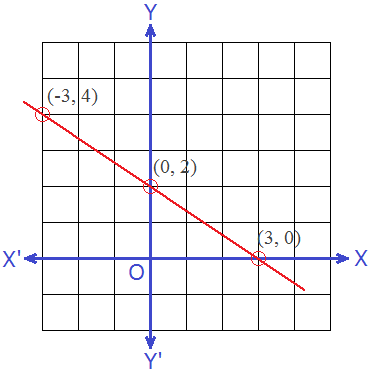
∴ Three solutions of the given linear equation 2x + 3y = 6 are (3,
0), (0, 2) and (-3, 4).
Now, plotting these points on a graph, and joining them by a straight line we get following graph of linear equation.
If you have any questions or problems regarding the Linear Equations in Two Variables, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: